On Lottery Tickets and Minimal Task Representations in Deep Reinforcement Learning
Paper and Code
May 31, 2021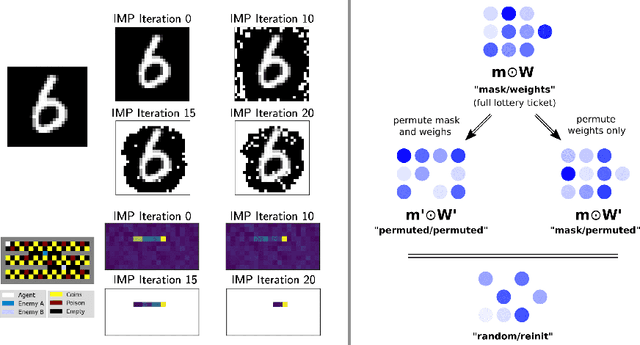
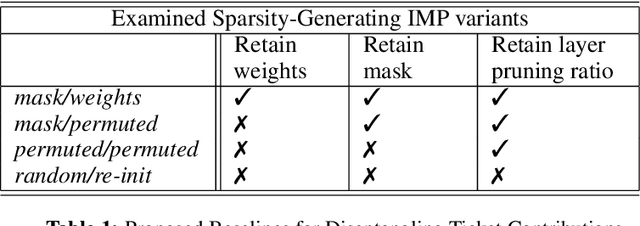
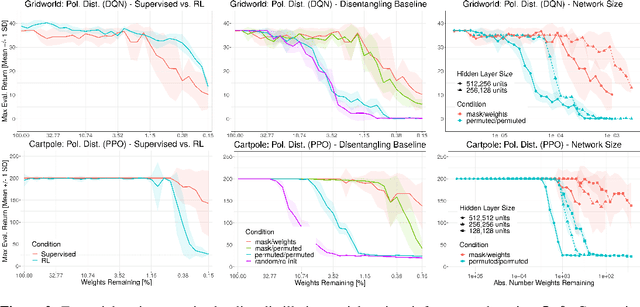
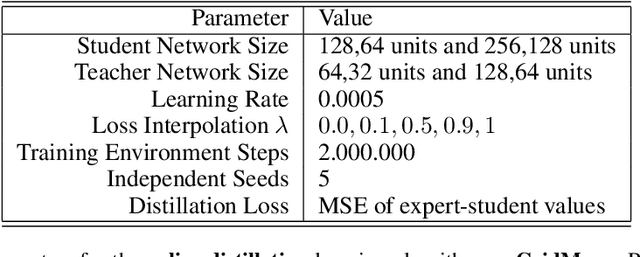
The lottery ticket hypothesis questions the role of overparameterization in supervised deep learning. But how is the performance of winning lottery tickets affected by the distributional shift inherent to reinforcement learning problems? In this work, we address this question by comparing sparse agents who have to address the non-stationarity of the exploration-exploitation problem with supervised agents trained to imitate an expert. We show that feed-forward networks trained via reinforcement learning and imitation learning can be pruned to the same level of sparsity, suggesting that the distributional shift has a limited impact on the size of winning tickets. Using a set of carefully designed baseline conditions, we find that the majority of the lottery ticket effect in both learning paradigms can be attributed to the identified mask rather than the weight initialization. The input layer mask selectively prunes entire input dimensions that turn out to be irrelevant for the task at hand. At a moderate level of sparsity the mask identified by iterative magnitude pruning yields minimal task-relevant representations, i.e., an interpretable inductive bias. Finally, we propose a simple initialization rescaling which promotes the robust identification of sparse task representations in low-dimensional control tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge