On Estimating Many Means, Selection Bias, and the Bootstrap
Paper and Code
Nov 15, 2013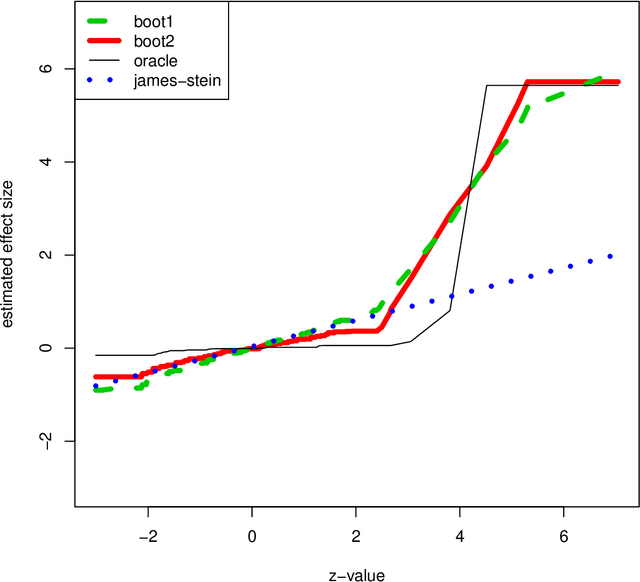



With recent advances in high throughput technology, researchers often find themselves running a large number of hypothesis tests (thousands+) and esti- mating a large number of effect-sizes. Generally there is particular interest in those effects estimated to be most extreme. Unfortunately naive estimates of these effect-sizes (even after potentially accounting for multiplicity in a testing procedure) can be severely biased. In this manuscript we explore this bias from a frequentist perspective: we give a formal definition, and show that an oracle estimator using this bias dominates the naive maximum likelihood estimate. We give a resampling estimator to approximate this oracle, and show that it works well on simulated data. We also connect this to ideas in empirical Bayes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge