On Enforcing Better Conditioned Meta-Learning for Rapid Few-Shot Adaptation
Paper and Code
Jun 15, 2022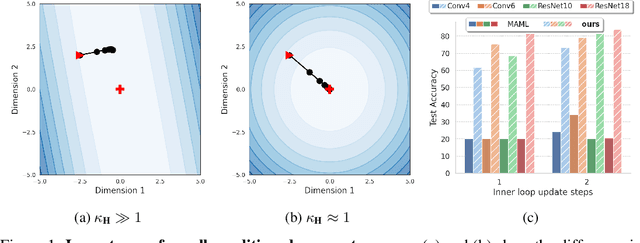

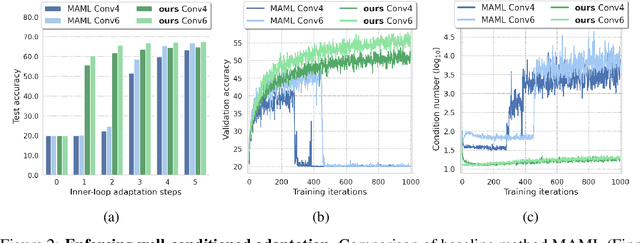
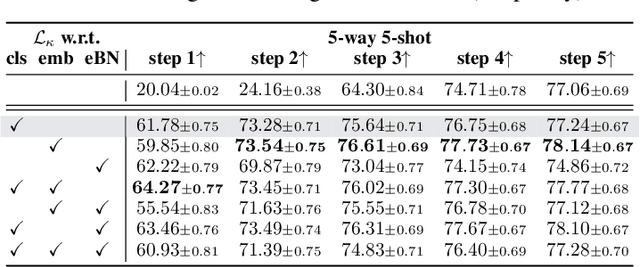
Inspired by the concept of preconditioning, we propose a novel method to increase adaptation speed for gradient-based meta-learning methods without incurring extra parameters. We demonstrate that recasting the optimization problem to a non-linear least-squares formulation provides a principled way to actively enforce a $\textit{well-conditioned}$ parameter space for meta-learning models based on the concepts of the condition number and local curvature. Our comprehensive evaluations show that the proposed method significantly outperforms its unconstrained counterpart especially during initial adaptation steps, while achieving comparable or better overall results on several few-shot classification tasks -- creating the possibility of dynamically choosing the number of adaptation steps at inference time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge