On Dropout and Nuclear Norm Regularization
Paper and Code
May 28, 2019
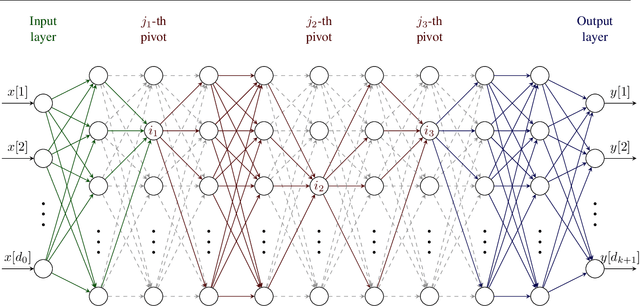
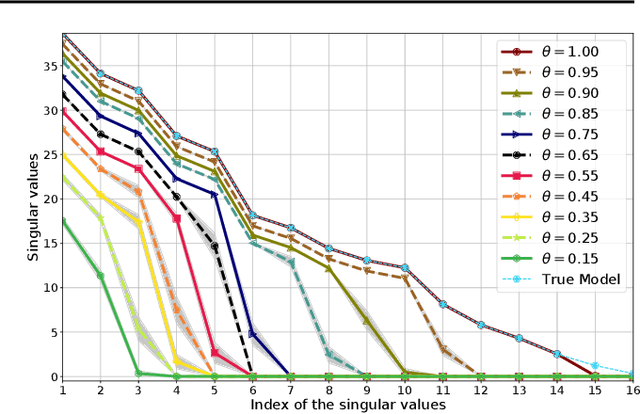
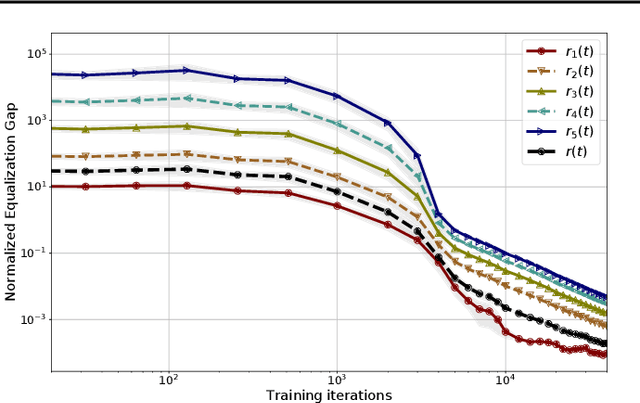
We give a formal and complete characterization of the explicit regularizer induced by dropout in deep linear networks with squared loss. We show that (a) the explicit regularizer is composed of an $\ell_2$-path regularizer and other terms that are also re-scaling invariant, (b) the convex envelope of the induced regularizer is the squared nuclear norm of the network map, and (c) for a sufficiently large dropout rate, we characterize the global optima of the dropout objective. We validate our theoretical findings with empirical results.
* Proceedings of the 36th International Conference on Machine
Learning, PMLR 97:4575-4584, 2019
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge