On Approximate Nonlinear Gaussian Message Passing On Factor Graphs
Paper and Code
Mar 21, 2019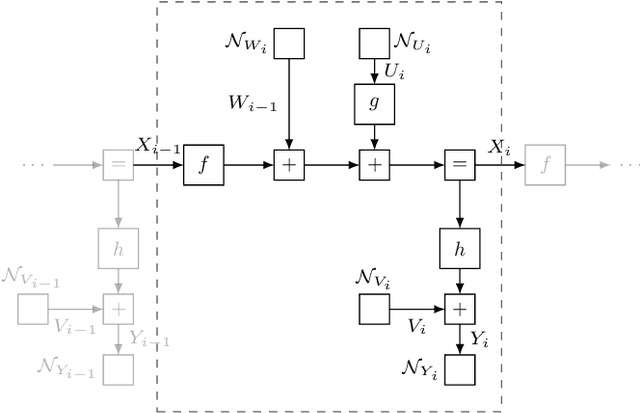


Factor graphs have recently gained increasing attention as a unified framework for representing and constructing algorithms for signal processing, estimation, and control. One capability that does not seem to be well explored within the factor graph tool kit is the ability to handle deterministic nonlinear transformations, such as those occurring in nonlinear filtering and smoothing problems, using tabulated message passing rules. In this contribution, we provide general forward (filtering) and backward (smoothing) approximate Gaussian message passing rules for deterministic nonlinear transformation nodes in arbitrary factor graphs fulfilling a Markov property, based on numerical quadrature procedures for the forward pass and a Rauch-Tung-Striebel-type approximation of the backward pass. These message passing rules can be employed for deriving many algorithms for solving nonlinear problems using factor graphs, as is illustrated by the proposition of a nonlinear modified Bryson-Frazier (MBF) smoother based on the presented message passing rules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge