On Anomaly Ranking and Excess-Mass Curves
Paper and Code
Feb 05, 2015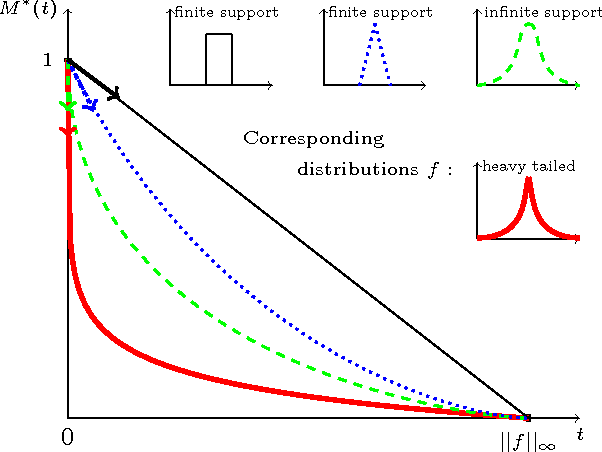
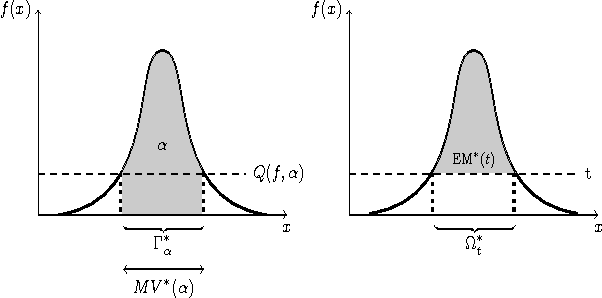
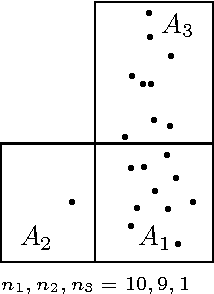
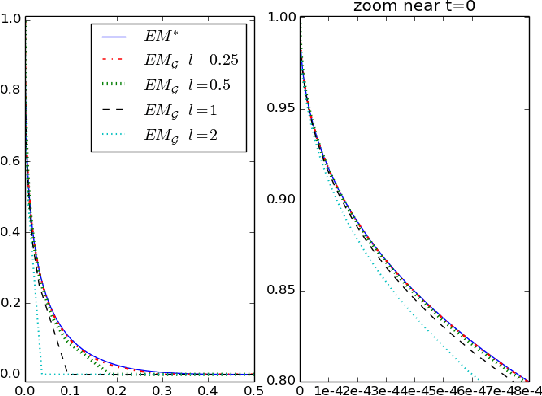
Learning how to rank multivariate unlabeled observations depending on their degree of abnormality/novelty is a crucial problem in a wide range of applications. In practice, it generally consists in building a real valued "scoring" function on the feature space so as to quantify to which extent observations should be considered as abnormal. In the 1-d situation, measurements are generally considered as "abnormal" when they are remote from central measures such as the mean or the median. Anomaly detection then relies on tail analysis of the variable of interest. Extensions to the multivariate setting are far from straightforward and it is precisely the main purpose of this paper to introduce a novel and convenient (functional) criterion for measuring the performance of a scoring function regarding the anomaly ranking task, referred to as the Excess-Mass curve (EM curve). In addition, an adaptive algorithm for building a scoring function based on unlabeled data X1 , . . . , Xn with a nearly optimal EM is proposed and is analyzed from a statistical perspective.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge