Off-policy reinforcement learning for $ H_\infty $ control design
Paper and Code
May 11, 2014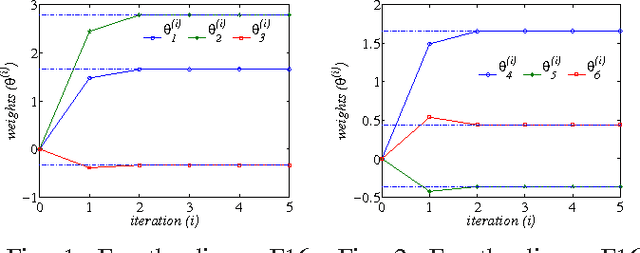
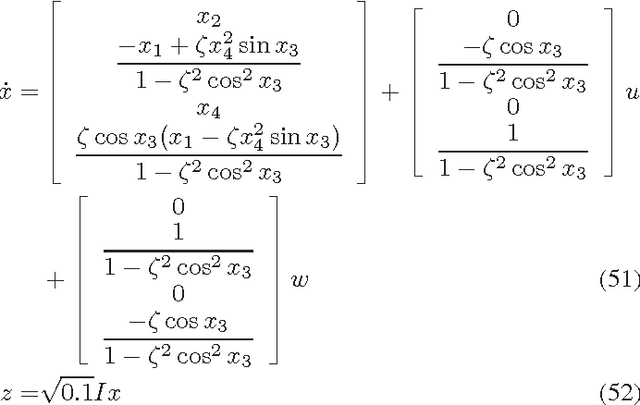
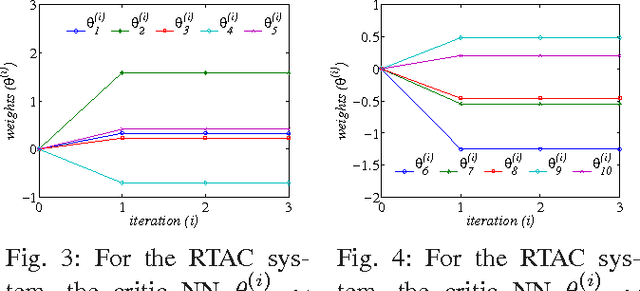
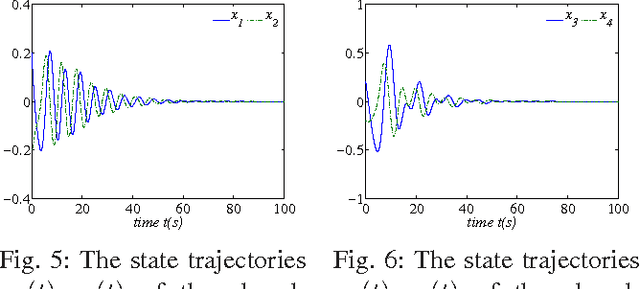
The $H_\infty$ control design problem is considered for nonlinear systems with unknown internal system model. It is known that the nonlinear $ H_\infty $ control problem can be transformed into solving the so-called Hamilton-Jacobi-Isaacs (HJI) equation, which is a nonlinear partial differential equation that is generally impossible to be solved analytically. Even worse, model-based approaches cannot be used for approximately solving HJI equation, when the accurate system model is unavailable or costly to obtain in practice. To overcome these difficulties, an off-policy reinforcement leaning (RL) method is introduced to learn the solution of HJI equation from real system data instead of mathematical system model, and its convergence is proved. In the off-policy RL method, the system data can be generated with arbitrary policies rather than the evaluating policy, which is extremely important and promising for practical systems. For implementation purpose, a neural network (NN) based actor-critic structure is employed and a least-square NN weight update algorithm is derived based on the method of weighted residuals. Finally, the developed NN-based off-policy RL method is tested on a linear F16 aircraft plant, and further applied to a rotational/translational actuator system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge