Obstacle Aware Sampling for Path Planning
Paper and Code
Mar 08, 2022
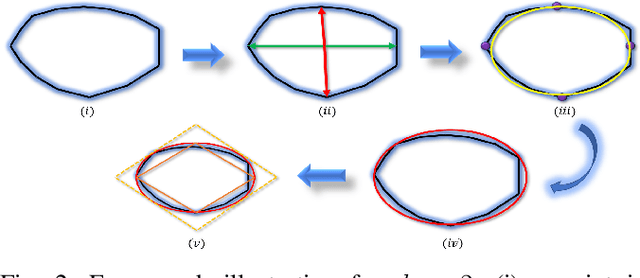
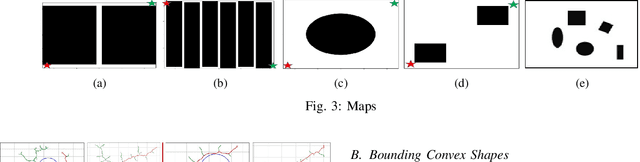
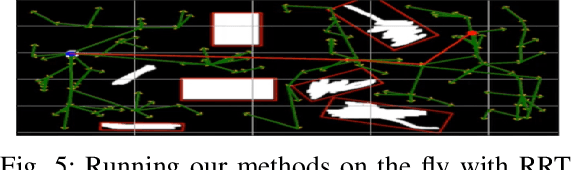
Many path planning algorithms are based on sampling the state space. While this approach is very simple, it can become costly when the obstacles are unknown, since samples hitting these obstacles are wasted. The goal of this paper is to efficiently identify obstacles in a map and remove them from the sampling space. To this end, we propose a pre-processing algorithm for space exploration that enables more efficient sampling. We show that it can boost the performance of other space sampling methods and path planners. Our approach is based on the fact that a convex obstacle can be approximated provably well by its minimum volume enclosing ellipsoid (MVEE), and a non-convex obstacle may be partitioned into convex shapes. Our main contribution is an algorithm that strategically finds a small sample, called the \emph{active-coreset}, that adaptively samples the space via membership-oracle such that the MVEE of the coreset approximates the MVEE of the obstacle. Experimental results confirm the effectiveness of our approach across multiple planners based on Rapidly-exploring random trees, showing significant improvement in terms of time and path length.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge