Object Representations as Fixed Points: Training Iterative Refinement Algorithms with Implicit Differentiation
Paper and Code
Jul 02, 2022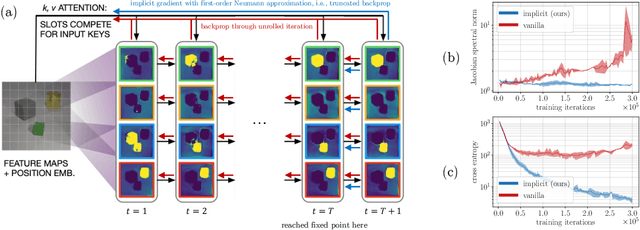

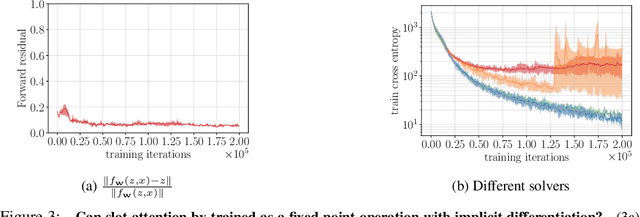
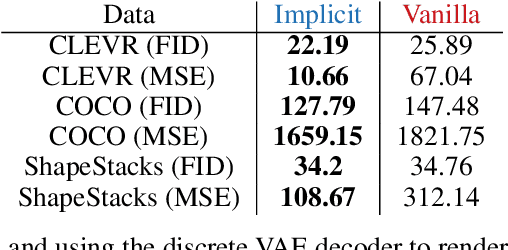
Iterative refinement -- start with a random guess, then iteratively improve the guess -- is a useful paradigm for representation learning because it offers a way to break symmetries among equally plausible explanations for the data. This property enables the application of such methods to infer representations of sets of entities, such as objects in physical scenes, structurally resembling clustering algorithms in latent space. However, most prior works differentiate through the unrolled refinement process, which can make optimization challenging. We observe that such methods can be made differentiable by means of the implicit function theorem, and develop an implicit differentiation approach that improves the stability and tractability of training by decoupling the forward and backward passes. This connection enables us to apply advances in optimizing implicit layers to not only improve the optimization of the slot attention module in SLATE, a state-of-the-art method for learning entity representations, but do so with constant space and time complexity in backpropagation and only one additional line of code.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge