Numerical Integration on Graphs: where to sample and how to weigh
Paper and Code
Mar 19, 2018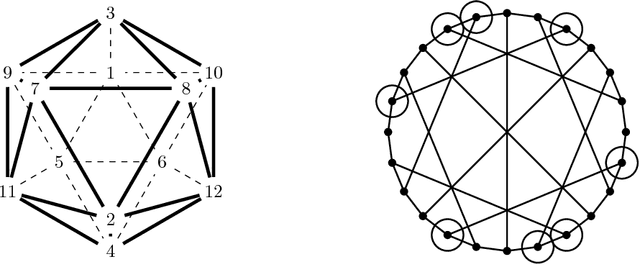
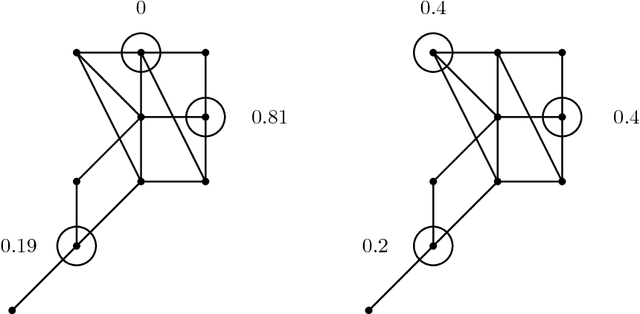
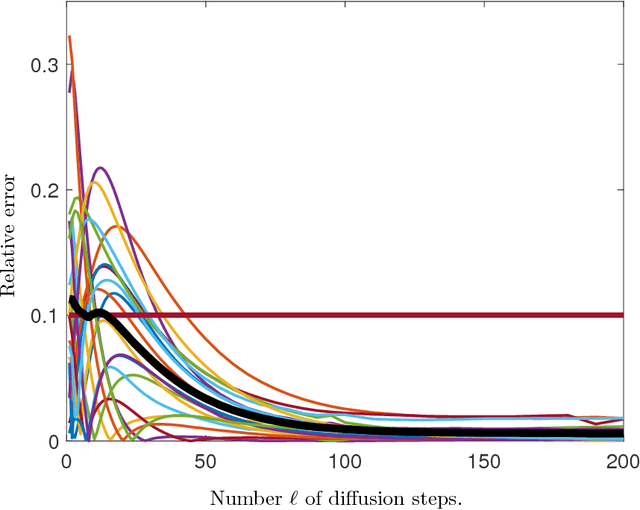
Let $G=(V,E,w)$ be a finite, connected graph with weighted edges. We are interested in the problem of finding a subset $W \subset V$ of vertices and weights $a_w$ such that $$ \frac{1}{|V|}\sum_{v \in V}^{}{f(v)} \sim \sum_{w \in W}{a_w f(w)}$$ for functions $f:V \rightarrow \mathbb{R}$ that are `smooth' with respect to the geometry of the graph. The main application are problems where $f$ is known to somehow depend on the underlying graph but is expensive to evaluate on even a single vertex. We prove an inequality showing that the integration problem can be rewritten as a geometric problem (`the optimal packing of heat balls'). We discuss how one would construct approximate solutions of the heat ball packing problem; numerical examples demonstrate the efficiency of the method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge