NPSA: Nonorthogonal Principal Skewness Analysis
Paper and Code
Jul 23, 2019

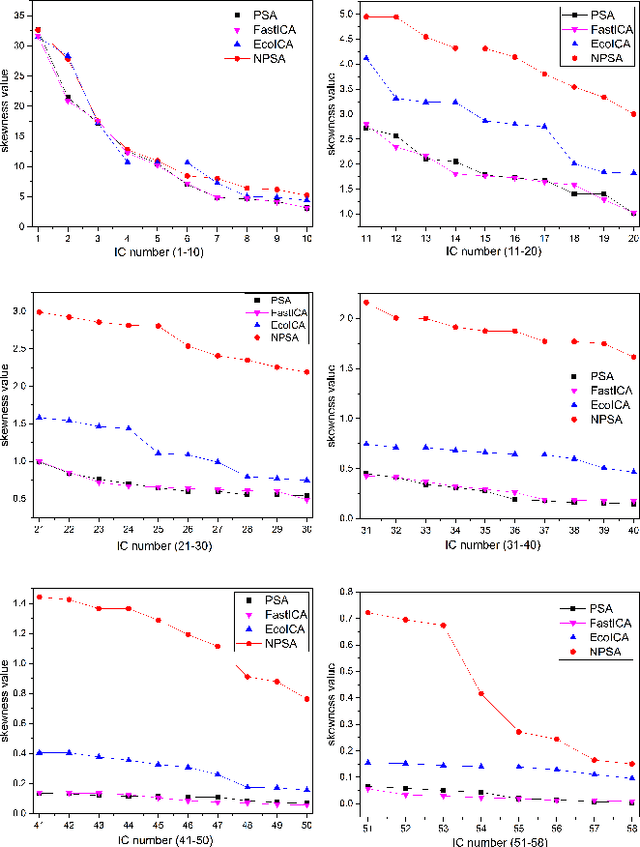
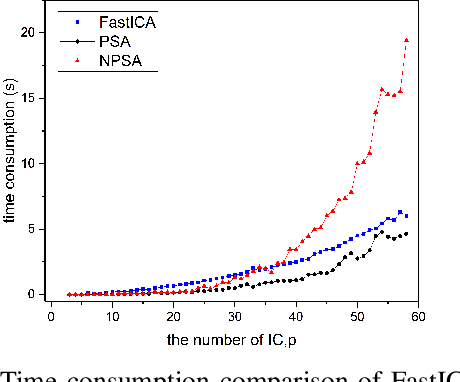
Principal skewness analysis (PSA) has been introduced for feature extraction in hyperspectral imagery. As a third-order generalization of principal component analysis (PCA), its solution of searching for the locally maximum skewness direction is transformed into the problem of calculating the eigenpairs (the eigenvalues and the corresponding eigenvectors) of a coskewness tensor. By combining a fixed-point method with an orthogonal constraint, it can prevent the new eigenpairs from converging to the same maxima that has been determined before. However, the eigenvectors of the supersymmetric tensor are not inherently orthogonal in general, which implies that the results obtained by the search strategy used in PSA may unavoidably deviate from the actual eigenpairs. In this paper, we propose a new nonorthogonal search strategy to solve this problem and the new algorithm is named nonorthogonal principal skewness analysis (NPSA). The contribution of NPSA lies in the finding that the search space of the eigenvector to be determined can be enlarged by using the orthogonal complement of the Kronecker product of the previous one, instead of its orthogonal complement space. We give a detailed theoretical proof to illustrate why the new strategy can result in the more accurate eigenpairs. In addition, after some algebraic derivations, the complexity of the presented algorithm is also greatly reduced. Experiments with both simulated data and real multi/hyperspectral imagery demonstrate its validity in feature extraction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge