Novel techniques for improvement the NNetEn entropy calculation for short and noisy time series

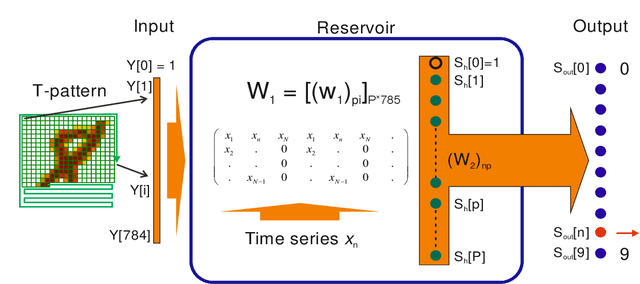
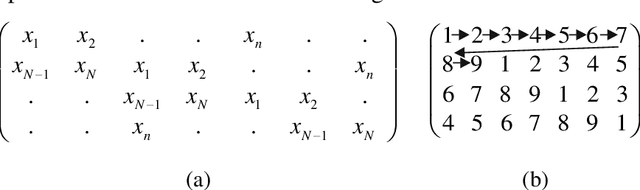
Entropy is a fundamental concept of information theory. It is widely used in the analysis of analog and digital signals. Conventional entropy measures have drawbacks, such as sensitivity to the length and amplitude of time series and low robustness to external noise. Recently, the NNetEn entropy measure has been introduced to overcome these problems. The NNetEn entropy uses a modified version of the LogNNet neural network classification model. The algorithm contains a reservoir matrix with N = 19625 elements, which the given time series should fill. Many practical time series have less than 19625 elements. Against this background, this paper investigates different duplicating and stretching techniques for filling to overcome this difficulty. The most successful technique is identified for practical applications. The presence of external noise and bias are other important issues affecting the efficiency of entropy measures. In order to perform meaningful analysis, three time series with different dynamics (chaotic, periodic, and binary), with a variation of signal-to-noise ratio (SNR) and offsets, are considered. It is shown that the error in the calculation of the NNetEn entropy does not exceed 10% when the SNR exceeds 30 dB. This opens the possibility of measuring the NNetEn of experimental signals in the presence of noise of various nature, white noise, or 1/f noise, without the need for noise filtering.