Novel Single View Constraints for Manhattan 3D Line Reconstruction
Paper and Code
Oct 08, 2018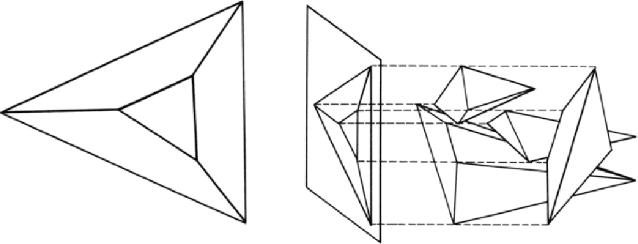

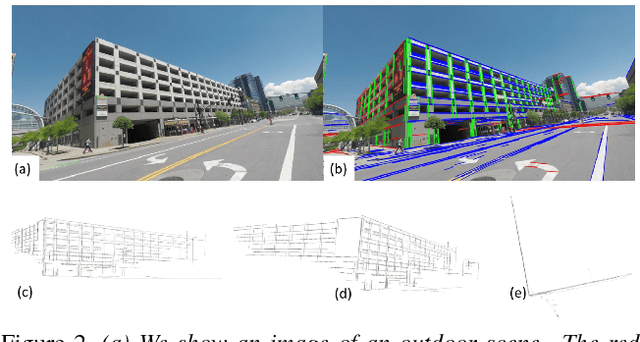

This paper proposes a novel and exact method to reconstruct line-based 3D structure from a single image using Manhattan world assumption. This problem is a distinctly unsolved problem because there can be multiple 3D reconstructions from a single image. Thus, we are often forced to look for priors like Manhattan world assumption and common scene structures. In addition to the standard orthogonality, perspective projection, and parallelism constraints, we investigate a few novel constraints based on the physical realizability of the 3D scene structure. We treat the line segments in the image to be part of a graph similar to straws and connectors game, where the goal is to back-project the line segments in 3D space and while ensuring that some of these 3D line segments connect with each other (i.e., truly intersect in 3D space) to form the 3D structure. We consider three sets of novel constraints while solving the reconstruction: (1) constraints on a series of Manhattan line intersections that form cycles, but are not all physically realizable, (2) constraints on true and false intersections in the case of nearby lines lying on the same Manhattan plane, and (3) constraints from the intersections on boundary and non-boundary line segments. The reconstruction is achieved using mixed integer linear programming (MILP), and we show compelling results on real images. Along with this paper, we will release a challenging Single View Line Reconstruction dataset with ground truth 3D line models for research purposes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge