Nostalgic Adam: Weighing more of the past gradients when designing the adaptive learning rate

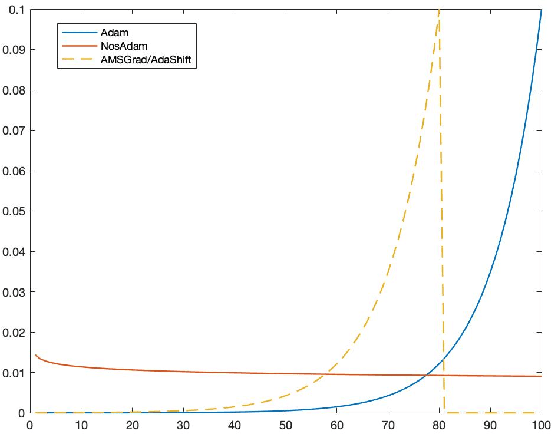
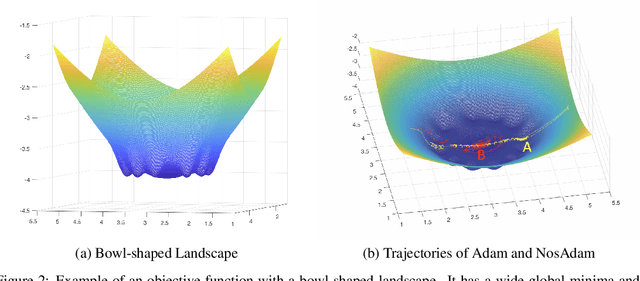
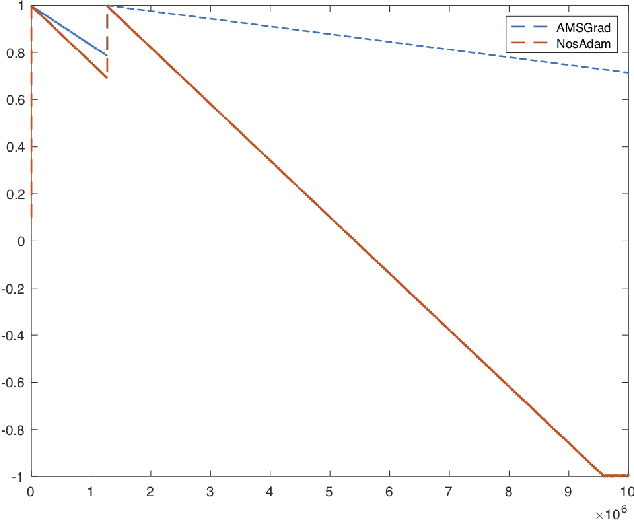
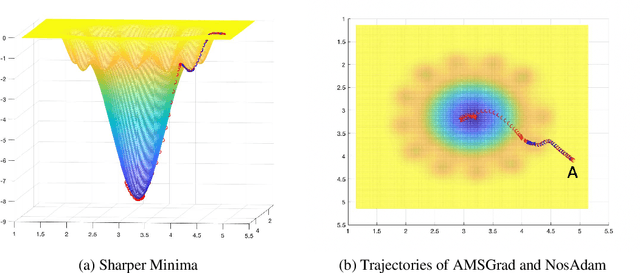
First-order optimization methods have been playing a prominent role in deep learning. Algorithms such as RMSProp and Adam are rather popular in training deep neural networks on large datasets. Recently, Reddi et al. discovered a flaw in the proof of convergence of Adam, and the authors proposed an alternative algorithm, AMSGrad, which has guaranteed convergence under certain conditions. In this paper, we propose a new algorithm, called Nostalgic Adam (NosAdam), which places bigger weights on the past gradients than the recent gradients when designing the adaptive learning rate. This is a new observation made through mathematical analysis of the algorithm. We also show that the estimate of the second moment of the gradient in NosAdam vanishes slower than Adam, which may account for faster convergence of NosAdam. We analyze the convergence of NosAdam and discover a convergence rate that achieves the best known convergence rate $O(1/\sqrt{T})$ for general convex online learning problems. Empirically, we show that NosAdam outperforms AMSGrad and Adam in some common machine learning problems.