Normalizing field flows: Solving forward and inverse stochastic differential equations using physics-informed flow models
Paper and Code
Sep 07, 2021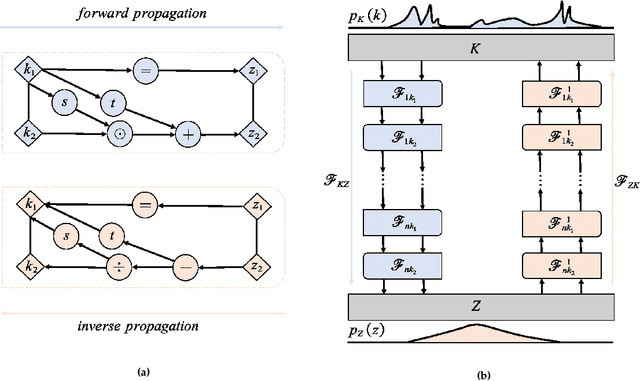

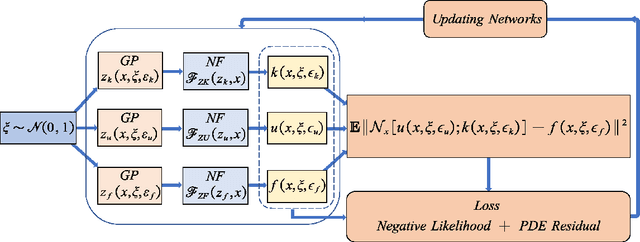
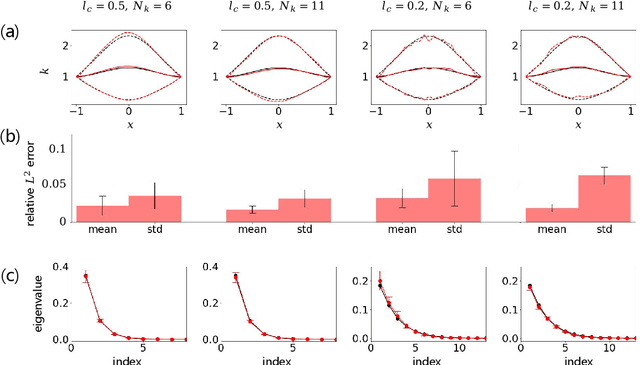
We introduce in this work the normalizing field flows (NFF) for learning random fields from scattered measurements. More precisely, we construct a bijective transformation (a normalizing flow characterizing by neural networks) between a Gaussian random field with the Karhunen-Lo\`eve (KL) expansion structure and the target stochastic field, where the KL expansion coefficients and the invertible networks are trained by maximizing the sum of the log-likelihood on scattered measurements. This NFF model can be used to solve data-driven forward, inverse, and mixed forward/inverse stochastic partial differential equations in a unified framework. We demonstrate the capability of the proposed NFF model for learning Non Gaussian processes and different types of stochastic partial differential equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge