Normalized Attention Without Probability Cage
Paper and Code
May 19, 2020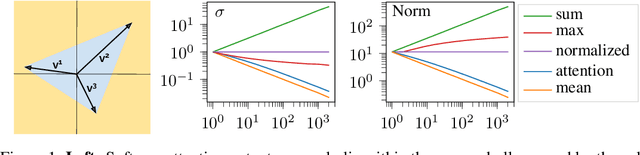
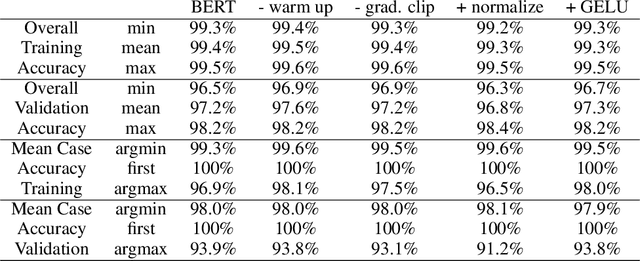
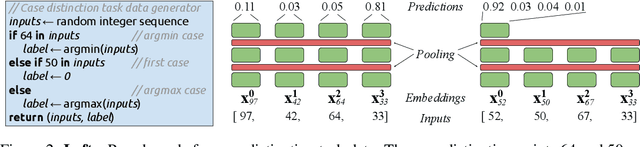

Attention architectures are widely used; they recently gained renewed popularity with Transformers yielding a streak of state of the art results. Yet, the geometrical implications of softmax-attention remain largely unexplored. In this work we highlight the limitations of constraining attention weights to the probability simplex and the resulting convex hull of value vectors. We show that Transformers are sequence length dependent biased towards token isolation at initialization and contrast Transformers to simple max- and sum-pooling - two strong baselines rarely reported. We propose to replace the softmax in self-attention with normalization, yielding a hyperparameter and data-bias robust, generally applicable architecture. We support our insights with empirical results from more than 25,000 trained models. All results and implementations are made available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge