Nonparametric mixture of Gaussian graphical models

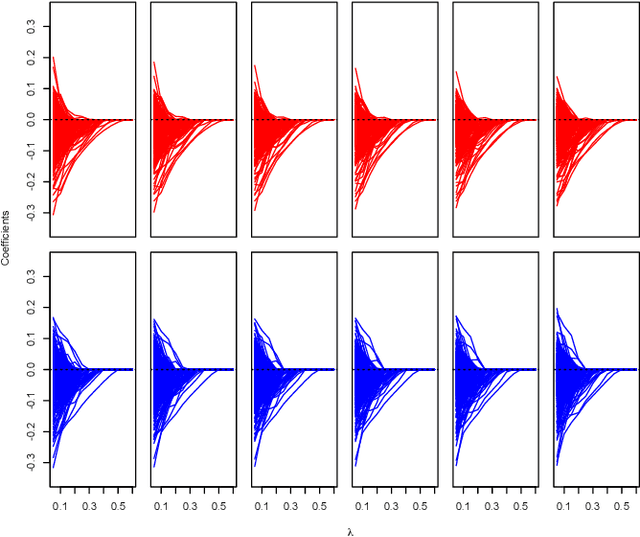
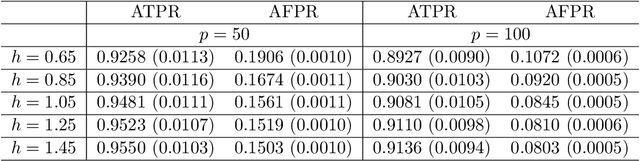
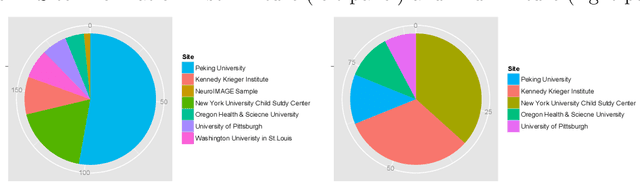
Graphical model has been widely used to investigate the complex dependence structure of high-dimensional data, and it is common to assume that observed data follow a homogeneous graphical model. However, observations usually come from different resources and have heterogeneous hidden commonality in real-world applications. Thus, it is of great importance to estimate heterogeneous dependencies and discover subpopulation with certain commonality across the whole population. In this work, we introduce a novel regularized estimation scheme for learning nonparametric mixture of Gaussian graphical models, which extends the methodology and applicability of Gaussian graphical models and mixture models. We propose a unified penalized likelihood approach to effectively estimate nonparametric functional parameters and heterogeneous graphical parameters. We further design an efficient generalized effective EM algorithm to address three significant challenges: high-dimensionality, non-convexity, and label switching. Theoretically, we study both the algorithmic convergence of our proposed algorithm and the asymptotic properties of our proposed estimators. Numerically, we demonstrate the performance of our method in simulation studies and a real application to estimate human brain functional connectivity from ADHD imaging data, where two heterogeneous conditional dependencies are explained through profiling demographic variables and supported by existing scientific findings.