Nonlinear Spatial Filtering in Multichannel Speech Enhancement
Paper and Code
Apr 22, 2021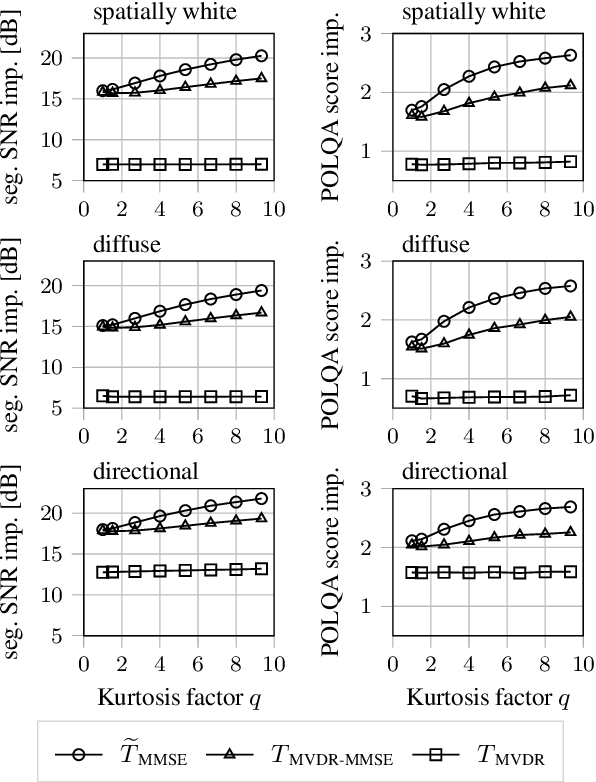
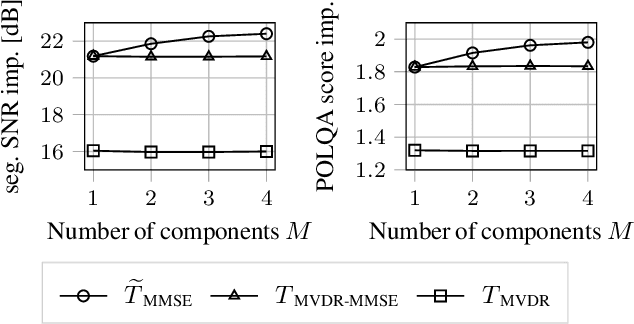
The majority of multichannel speech enhancement algorithms are two-step procedures that first apply a linear spatial filter, a so-called beamformer, and combine it with a single-channel approach for postprocessing. However, the serial concatenation of a linear spatial filter and a postfilter is not generally optimal in the minimum mean square error (MMSE) sense for noise distributions other than a Gaussian distribution. Rather, the MMSE optimal filter is a joint spatial and spectral nonlinear function. While estimating the parameters of such a filter with traditional methods is challenging, modern neural networks may provide an efficient way to learn the nonlinear function directly from data. To see if further research in this direction is worthwhile, in this work we examine the potential performance benefit of replacing the common two-step procedure with a joint spatial and spectral nonlinear filter. We analyze three different forms of non-Gaussianity: First, we evaluate on super-Gaussian noise with a high kurtosis. Second, we evaluate on inhomogeneous noise fields created by five interfering sources using two microphones, and third, we evaluate on real-world recordings from the CHiME3 database. In all scenarios, considerable improvements may be obtained. Most prominently, our analyses show that a nonlinear spatial filter uses the available spatial information more effectively than a linear spatial filter as it is capable of suppressing more than $D-1$ directional interfering sources with a $D$-dimensional microphone array without spatial adaptation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge