Nonlinear Eigenproblems in Data Analysis - Balanced Graph Cuts and the RatioDCA-Prox
Paper and Code
Mar 24, 2014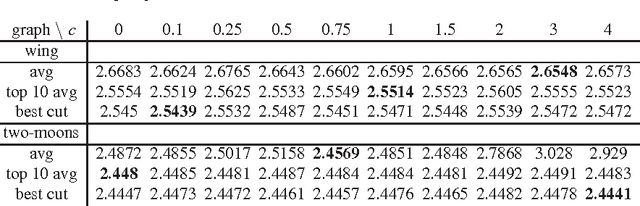
It has been recently shown that a large class of balanced graph cuts allows for an exact relaxation into a nonlinear eigenproblem. We review briefly some of these results and propose a family of algorithms to compute nonlinear eigenvectors which encompasses previous work as special cases. We provide a detailed analysis of the properties and the convergence behavior of these algorithms and then discuss their application in the area of balanced graph cuts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge