Non-Negative Local Sparse Coding for Subspace Clustering
Paper and Code
Mar 12, 2019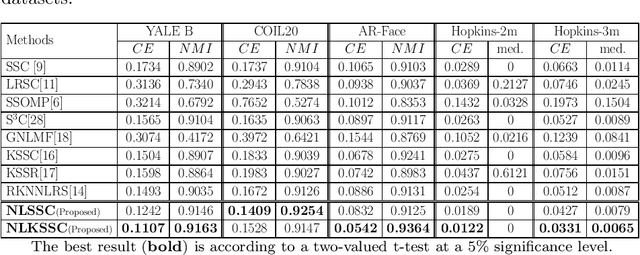

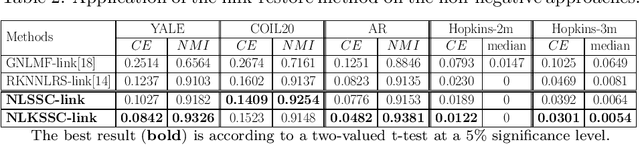

Subspace sparse coding (SSC) algorithms have proven to be beneficial to clustering problems. They provide an alternative data representation in which the underlying structure of the clusters can be better captured. However, most of the research in this area is mainly focused on enhancing the sparse coding part of the problem. In contrast, we introduce a novel objective term in our proposed SSC framework which focuses on the separability of data points in the coding space. We also provide mathematical insights into how this local-separability term improves the clustering result of the SSC framework. Our proposed non-linear local SSC algorithm (NLSSC) also benefits from the efficient choice of its sparsity terms and constraints. The NLSSC algorithm is also formulated in the kernel-based framework (NLKSSC) which can represent the nonlinear structure of data. In addition, we address the possibility of having redundancies in sparse coding results and its negative effect on graph-based clustering problems. We introduce the link-restore post-processing step to improve the representation graph of non-negative SSC algorithms such as ours. Empirical evaluations on well-known clustering benchmarks show that our proposed NLSSC framework results in better clusterings compared to the state-of-the-art baselines and demonstrate the effectiveness of the link-restore post-processing in improving the clustering accuracy via correcting the broken links of the representation graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge