Non-asymptotic Convergence of Training Transformers for Next-token Prediction
Paper and Code
Sep 25, 2024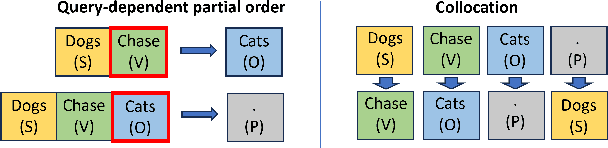
Transformers have achieved extraordinary success in modern machine learning due to their excellent ability to handle sequential data, especially in next-token prediction (NTP) tasks. However, the theoretical understanding of their performance in NTP is limited, with existing studies focusing mainly on asymptotic performance. This paper provides a fine-grained non-asymptotic analysis of the training dynamics of a one-layer transformer consisting of a self-attention module followed by a feed-forward layer. We first characterize the essential structural properties of training datasets for NTP using a mathematical framework based on partial orders. Then, we design a two-stage training algorithm, where the pre-processing stage for training the feed-forward layer and the main stage for training the attention layer exhibit fast convergence performance. Specifically, both layers converge sub-linearly to the direction of their corresponding max-margin solutions. We also show that the cross-entropy loss enjoys a linear convergence rate. Furthermore, we show that the trained transformer presents non-trivial prediction ability with dataset shift, which sheds light on the remarkable generalization performance of transformers. Our analysis technique involves the development of novel properties on the attention gradient and further in-depth analysis of how these properties contribute to the convergence of the training process. Our experiments further validate our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge