Noise Estimation Is Not Optimal: How To Use Kalman Filter The Right Way
Paper and Code
May 04, 2021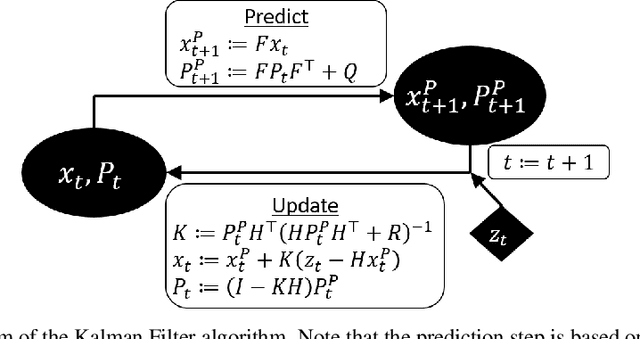
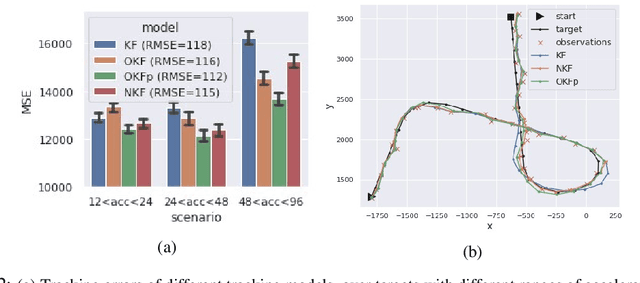
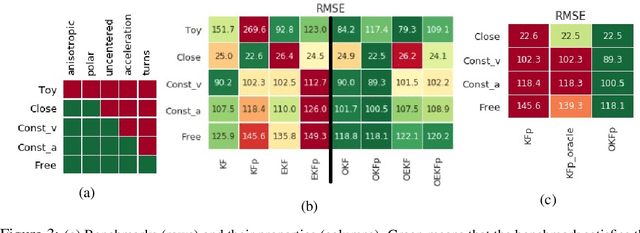
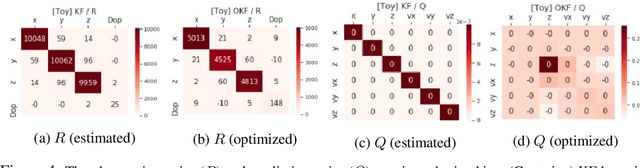
Determining the noise parameters of a Kalman Filter (KF) has been researched for decades. The research focuses on the task of estimation of the noise under various conditions, since precise noise estimation is considered equivalent to errors minimization. However, we show that even a small violation of KF assumptions can significantly modify the effective noise, breaking the equivalence between the tasks and making noise estimation an inferior strategy. We show that such violations are very common, and are often not trivial to handle or even notice. Consequentially, we argue that a robust solution is needed - rather than choosing a dedicated model per problem. To that end, we use a simple parameterization to apply gradient-based optimization efficiently to the symmetric and positive-definite parameters of KF. In radar tracking and video tracking, we show that the optimization improves both the accuracy of KF and its robustness to design decisions. In addition, we demonstrate how a neural network model can seem to reduce the errors significantly compared to a KF - and how this reduction vanishes once the KF is optimized. This indicates how complicated models can be wrongly identified as superior to KF, while in fact they were merely over-optimized.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge