No Shifted Augmentations (NSA): compact distributions for robust self-supervised Anomaly Detection
Paper and Code
Mar 19, 2022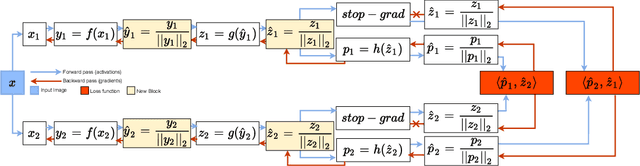
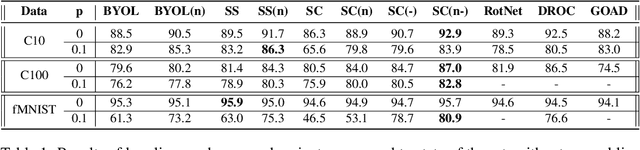
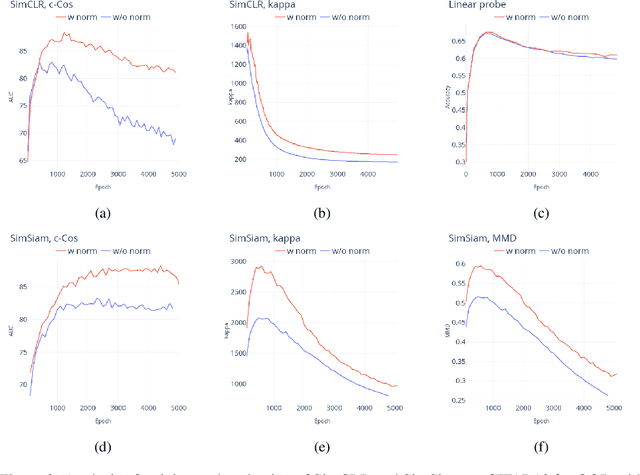
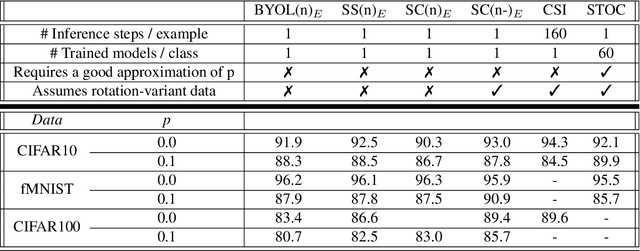
Unsupervised Anomaly detection (AD) requires building a notion of normalcy, distinguishing in-distribution (ID) and out-of-distribution (OOD) data, using only available ID samples. Recently, large gains were made on this task for the domain of natural images using self-supervised contrastive feature learning as a first step followed by kNN or traditional one-class classifiers for feature scoring. Learned representations that are non-uniformly distributed on the unit hypersphere have been shown to be beneficial for this task. We go a step further and investigate how the \emph {geometrical compactness} of the ID feature distribution makes isolating and detecting outliers easier, especially in the realistic situation when ID training data is polluted (i.e. ID data contains some OOD data that is used for learning the feature extractor parameters). We propose novel architectural modifications to the self-supervised feature learning step, that enable such compact distributions for ID data to be learned. We show that the proposed modifications can be effectively applied to most existing self-supervised objectives, with large gains in performance. Furthermore, this improved OOD performance is obtained without resorting to tricks such as using strongly augmented ID images (e.g. by 90 degree rotations) as proxies for the unseen OOD data, as these impose overly prescriptive assumptions about ID data and its invariances. We perform extensive studies on benchmark datasets for one-class OOD detection and show state-of-the-art performance in the presence of pollution in the ID data, and comparable performance otherwise. We also propose and extensively evaluate a novel feature scoring technique based on the angular Mahalanobis distance, and propose a simple and novel technique for feature ensembling during evaluation that enables a big boost in performance at nearly zero run-time cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge