No-Regret Learning in Two-Echelon Supply Chain with Unknown Demand Distribution
Paper and Code
Oct 23, 2022
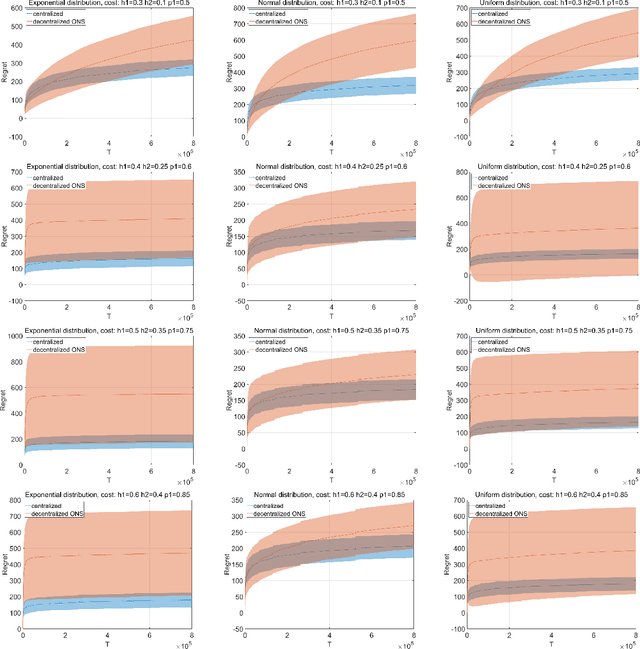
Supply chain management (SCM) has been recognized as an important discipline with applications to many industries, where the two-echelon stochastic inventory model, involving one downstream retailer and one upstream supplier, plays a fundamental role for developing firms' SCM strategies. In this work, we aim at designing online learning algorithms for this problem with an unknown demand distribution, which brings distinct features as compared to classic online optimization problems. Specifically, we consider the two-echelon supply chain model introduced in [Cachon and Zipkin, 1999] under two different settings: the centralized setting, where a planner decides both agents' strategy simultaneously, and the decentralized setting, where two agents decide their strategy independently and selfishly. We design algorithms that achieve favorable guarantees for both regret and convergence to the optimal inventory decision in both settings, and additionally for individual regret in the decentralized setting. Our algorithms are based on Online Gradient Descent and Online Newton Step, together with several new ingredients specifically designed for our problem. We also implement our algorithms and show their empirical effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge