New Perspectives on k-Support and Cluster Norms
Paper and Code
Mar 06, 2014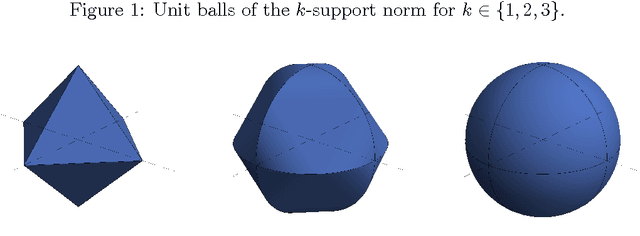

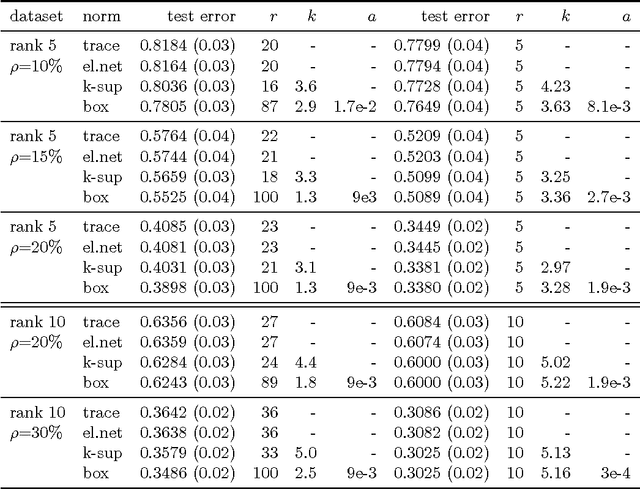

The $k$-support norm is a regularizer which has been successfully applied to sparse vector prediction problems. We show that it belongs to a general class of norms which can be formulated as a parameterized infimum over quadratics. We further extend the $k$-support norm to matrices, and we observe that it is a special case of the matrix cluster norm. Using this formulation we derive an efficient algorithm to compute the proximity operator of both norms. This improves upon the standard algorithm for the $k$-support norm and allows us to apply proximal gradient methods to the cluster norm. We also describe how to solve regularization problems which employ centered versions of these norms. Finally, we apply the matrix regularizers to different matrix completion and multitask learning datasets. Our results indicate that the spectral $k$-support norm and the cluster norm give state of the art performance on these problems, significantly outperforming trace norm and elastic net penalties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge