New Perspectives on $k$-Support and Cluster Norms
Paper and Code
Dec 27, 2015

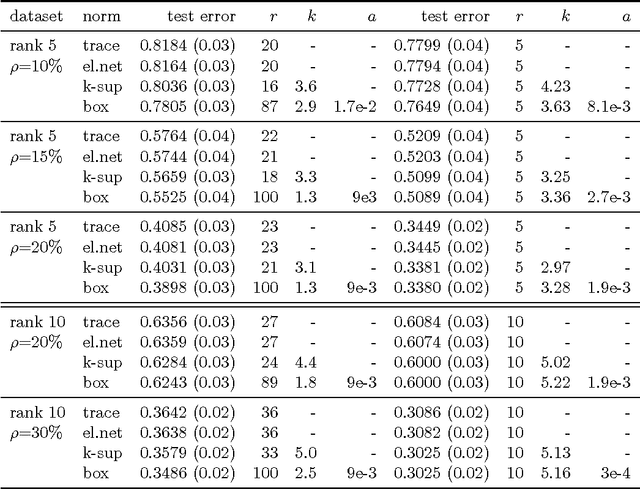

We study a regularizer which is defined as a parameterized infimum of quadratics, and which we call the box-norm. We show that the k-support norm, a regularizer proposed by [Argyriou et al, 2012] for sparse vector prediction problems, belongs to this family, and the box-norm can be generated as a perturbation of the former. We derive an improved algorithm to compute the proximity operator of the squared box-norm, and we provide a method to compute the norm. We extend the norms to matrices, introducing the spectral k-support norm and spectral box-norm. We note that the spectral box-norm is essentially equivalent to the cluster norm, a multitask learning regularizer introduced by [Jacob et al. 2009a], and which in turn can be interpreted as a perturbation of the spectral k-support norm. Centering the norm is important for multitask learning and we also provide a method to use centered versions of the norms as regularizers. Numerical experiments indicate that the spectral k-support and box-norms and their centered variants provide state of the art performance in matrix completion and multitask learning problems respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge