Neural tensor contractions and the expressive power of deep neural quantum states
Paper and Code
Mar 18, 2021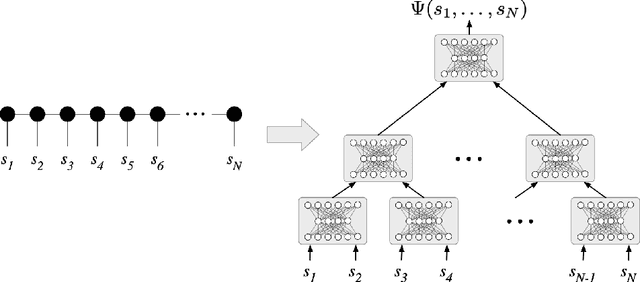


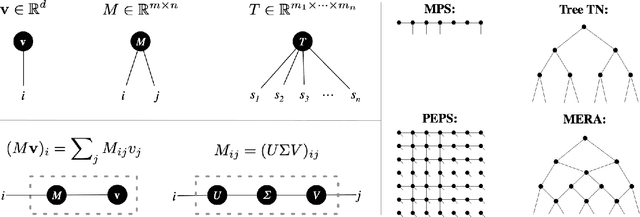
We establish a direct connection between general tensor networks and deep feed-forward artificial neural networks. The core of our results is the construction of neural-network layers that efficiently perform tensor contractions, and that use commonly adopted non-linear activation functions. The resulting deep networks feature a number of edges that closely matches the contraction complexity of the tensor networks to be approximated. In the context of many-body quantum states, this result establishes that neural-network states have strictly the same or higher expressive power than practically usable variational tensor networks. As an example, we show that all matrix product states can be efficiently written as neural-network states with a number of edges polynomial in the bond dimension and depth logarithmic in the system size. The opposite instead does not hold true, and our results imply that there exist quantum states that are not efficiently expressible in terms of matrix product states or practically usable PEPS, but that are instead efficiently expressible with neural network states.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge