Neural network training under semidefinite constraints

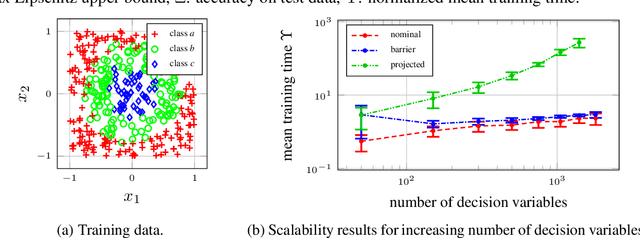
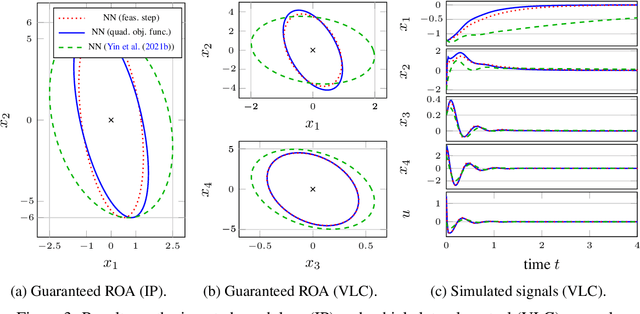
This paper is concerned with the training of neural networks (NNs) under semidefinite constraints. This type of training problems has recently gained popularity since semidefinite constraints can be used to verify interesting properties for NNs that include, e.g., the estimation of an upper bound on the Lipschitz constant, which relates to the robustness of an NN, or the stability of dynamic systems with NN controllers. The utilized semidefinite constraints are based on sector constraints satisfied by the underlying activation functions. Unfortunately, one of the biggest bottlenecks of these new results is the required computational effort for incorporating the semidefinite constraints into the training of NNs which is limiting their scalability to large NNs. We address this challenge by developing interior point methods for NN training that we implement using barrier functions for semidefinite constraints. In order to efficiently compute the gradients of the barrier terms, we exploit the structure of the semidefinite constraints. In experiments, we demonstrate the superior efficiency of our training method over previous approaches, which allows us, e.g., to use semidefinite constraints in the training of Wasserstein generative adversarial networks, where the discriminator must satisfy a Lipschitz condition.