Neural network is heterogeneous: Phase matters more

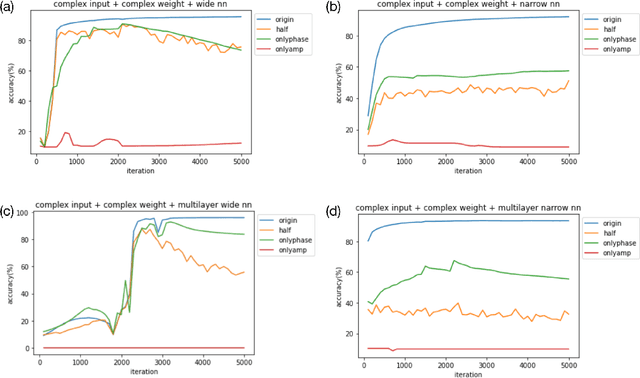
We find a heterogeneity in both complex and real valued neural networks with the insight from wave optics, claiming a much more important role of phase than its amplitude counterpart in the weight matrix. In complex-valued neural networks, we show that among different types of pruning, the weight matrix with only phase information preserved achieves the best accuracy, which holds robustly under various settings of depth and width. The conclusion can be generalized to real-valued neural networks, where signs take the place of phases. These inspiring findings enrich the techniques of network pruning and binary computation.