Neural Likelihoods for Multi-Output Gaussian Processes
Paper and Code
May 31, 2019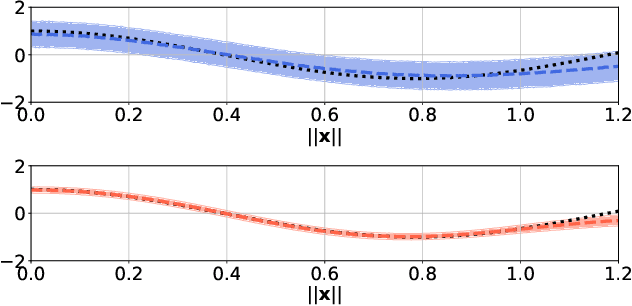
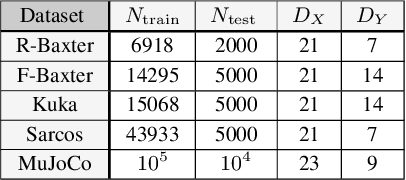
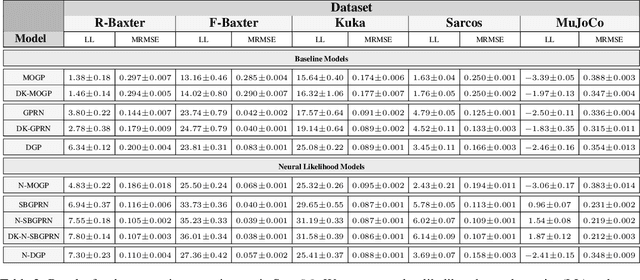
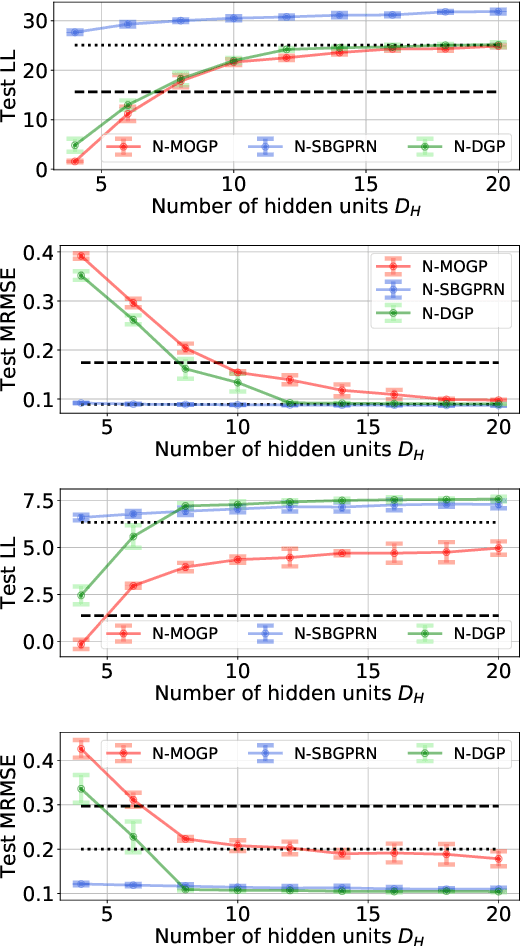
We construct flexible likelihoods for multi-output Gaussian process models that leverage neural networks as components. We make use of sparse variational inference methods to enable scalable approximate inference for the resulting class of models. An attractive feature of these models is that they can admit analytic predictive means even when the likelihood is non-linear and the predictive distributions are non-Gaussian. We validate the modeling potential of these models in a variety of experiments in both the supervised and unsupervised setting. We demonstrate that the flexibility of these `neural' likelihoods can improve prediction quality as compared to simpler Gaussian process models and that neural likelihoods can be readily combined with a variety of underlying Gaussian process models, including deep Gaussian processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge