Neural Learning of One-of-Many Solutions for Combinatorial Problems in Structured Output Spaces
Paper and Code
Aug 27, 2020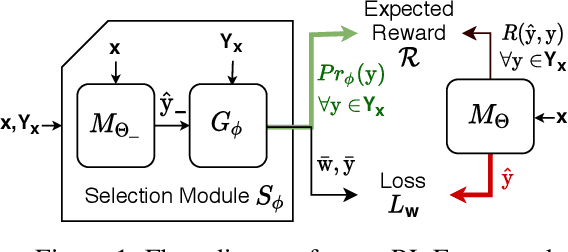

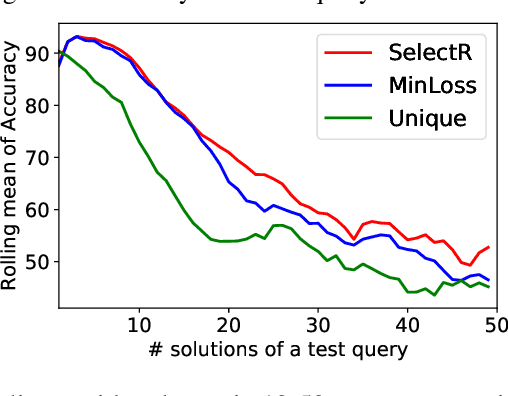
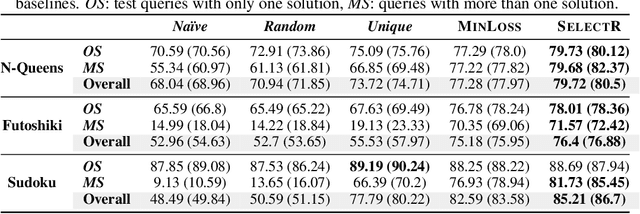
Recent research has proposed neural architectures for solving combinatorial problems in structured output spaces. In many such problems, there may exist multiple solutions for a given input, e.g. a partially filled Sudoku puzzle may have many completions satisfying all constraints. Further, we are often interested in finding {\em any one} of the possible solutions, without any preference between them. Existing approaches completely ignore this solution multiplicity. In this paper, we argue that being oblivious to the presence of multiple solutions can severely hamper their training ability. Our contribution is two fold. First, we formally define the task of learning one-of-many solutions for combinatorial problems in structured output spaces, which is applicable for solving several problems of interest such as N-Queens, and Sudoku. Second, we present a generic learning framework that adapts an existing prediction network for a combinatorial problem to handle solution multiplicity. Our framework uses a selection module, whose goal is to dynamically determine, for every input, the solution that is most effective for training the network parameters in any given learning iteration. We propose an RL based approach to jointly train the selection module with the prediction network. Experiments on three different domains, and using two different prediction networks, demonstrate that our framework significantly improves the accuracy in our setting, obtaining up to $21$ pt gain over the baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge