Neural Harmonium: An Interpretable Deep Structure for Nonlinear Dynamic System Identification with Application to Audio Processing
Paper and Code
Oct 10, 2023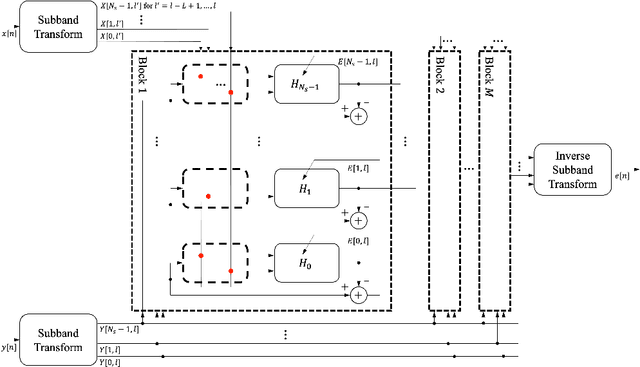
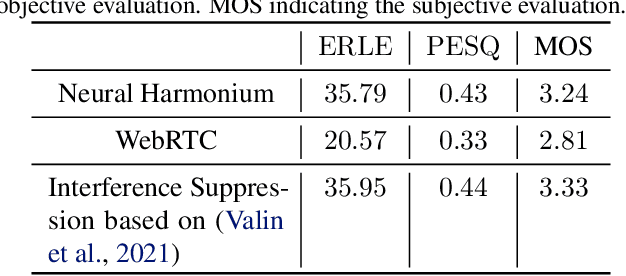
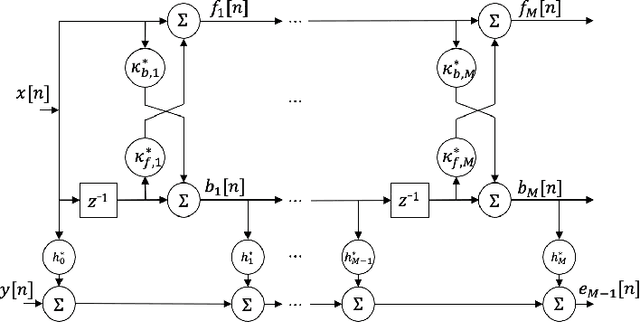

Improving the interpretability of deep neural networks has recently gained increased attention, especially when the power of deep learning is leveraged to solve problems in physics. Interpretability helps us understand a model's ability to generalize and reveal its limitations. In this paper, we introduce a causal interpretable deep structure for modeling dynamic systems. Our proposed model makes use of the harmonic analysis by modeling the system in a time-frequency domain while maintaining high temporal and spectral resolution. Moreover, the model is built in an order recursive manner which allows for fast, robust, and exact second order optimization without the need for an explicit Hessian calculation. To circumvent the resulting high dimensionality of the building blocks of our system, a neural network is designed to identify the frequency interdependencies. The proposed model is illustrated and validated on nonlinear system identification problems as required for audio signal processing tasks. Crowd-sourced experimentation contrasting the performance of the proposed approach to other state-of-the-art solutions on an acoustic echo cancellation scenario confirms the effectiveness of our method for real-life applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge