Neural Design for Genetic Perturbation Experiments
Paper and Code
Jul 26, 2022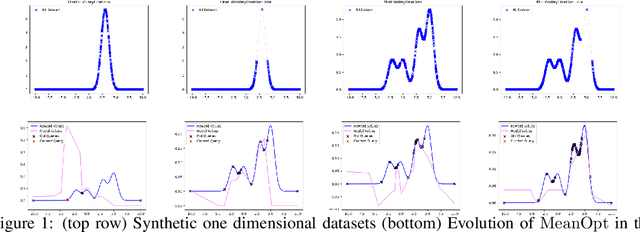
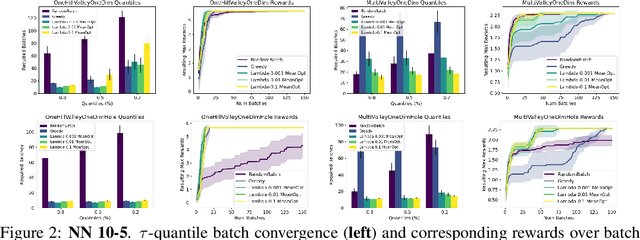
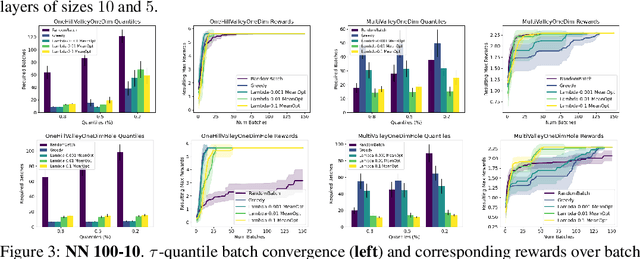

The problem of how to genetically modify cells in order to maximize a certain cellular phenotype has taken center stage in drug development over the last few years (with, for example, genetically edited CAR-T, CAR-NK, and CAR-NKT cells entering cancer clinical trials). Exhausting the search space for all possible genetic edits (perturbations) or combinations thereof is infeasible due to cost and experimental limitations. This work provides a theoretically sound framework for iteratively exploring the space of perturbations in pooled batches in order to maximize a target phenotype under an experimental budget. Inspired by this application domain, we study the problem of batch query bandit optimization and introduce the Optimistic Arm Elimination ($\mathrm{OAE}$) principle designed to find an almost optimal arm under different functional relationships between the queries (arms) and the outputs (rewards). We analyze the convergence properties of $\mathrm{OAE}$ by relating it to the Eluder dimension of the algorithm's function class and validate that $\mathrm{OAE}$ outperforms other strategies in finding optimal actions in experiments on simulated problems, public datasets well-studied in bandit contexts, and in genetic perturbation datasets when the regression model is a deep neural network. OAE also outperforms the benchmark algorithms in 3 of 4 datasets in the GeneDisco experimental planning challenge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge