Neural Continuous-Time Markov Models
Paper and Code
Dec 11, 2022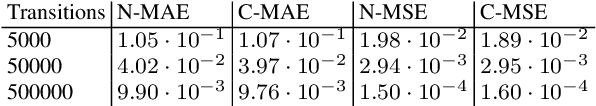
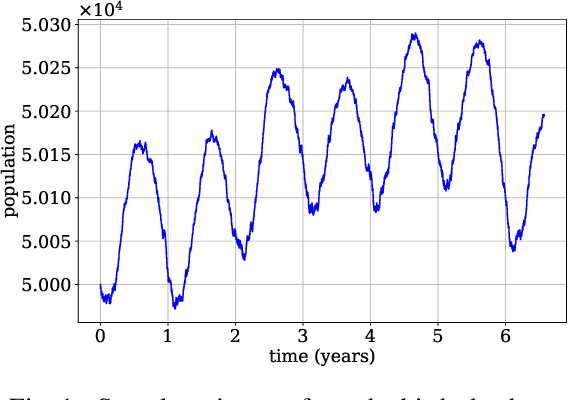
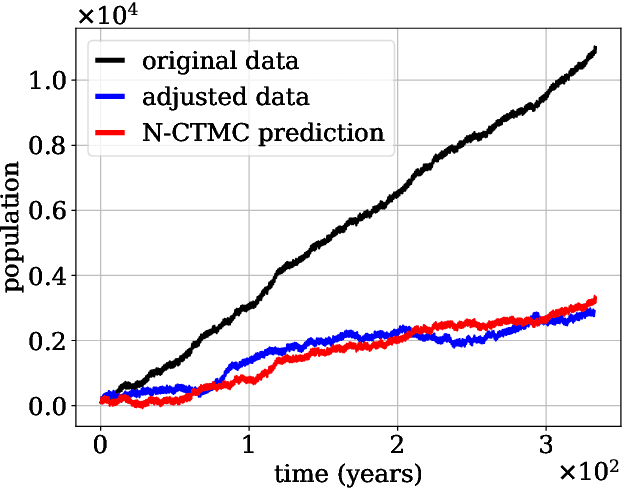
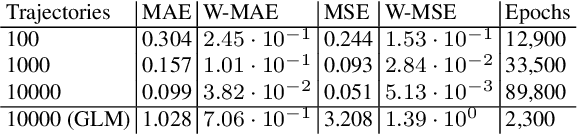
Continuous-time Markov chains are used to model stochastic systems where transitions can occur at irregular times, e.g., birth-death processes, chemical reaction networks, population dynamics, and gene regulatory networks. We develop a method to learn a continuous-time Markov chain's transition rate functions from fully observed time series. In contrast with existing methods, our method allows for transition rates to depend nonlinearly on both state variables and external covariates. The Gillespie algorithm is used to generate trajectories of stochastic systems where propensity functions (reaction rates) are known. Our method can be viewed as the inverse: given trajectories of a stochastic reaction network, we generate estimates of the propensity functions. While previous methods used linear or log-linear methods to link transition rates to covariates, we use neural networks, increasing the capacity and potential accuracy of learned models. In the chemical context, this enables the method to learn propensity functions from non-mass-action kinetics. We test our method with synthetic data generated from a variety of systems with known transition rates. We show that our method learns these transition rates with considerably more accuracy than log-linear methods, in terms of mean absolute error between ground truth and predicted transition rates. We also demonstrate an application of our methods to open-loop control of a continuous-time Markov chain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge