Neural Contextual Bandits via Reward-Biased Maximum Likelihood Estimation

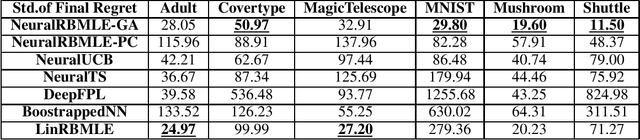
Reward-biased maximum likelihood estimation (RBMLE) is a classic principle in the adaptive control literature for tackling explore-exploit trade-offs. This paper studies the stochastic contextual bandit problem with general bounded reward functions and proposes NeuralRBMLE, which adapts the RBMLE principle by adding a bias term to the log-likelihood to enforce exploration. NeuralRBMLE leverages the representation power of neural networks and directly encodes exploratory behavior in the parameter space, without constructing confidence intervals of the estimated rewards. We propose two variants of NeuralRBMLE algorithms: The first variant directly obtains the RBMLE estimator by gradient ascent, and the second variant simplifies RBMLE to a simple index policy through an approximation. We show that both algorithms achieve $\widetilde{\mathcal{O}}(\sqrt{T})$ regret. Through extensive experiments, we demonstrate that the NeuralRBMLE algorithms achieve comparable or better empirical regrets than the state-of-the-art methods on real-world datasets with non-linear reward functions.