Network Volume Anomaly Detection and Identification in Large-scale Networks based on Online Time-structured Traffic Tensor Tracking
Paper and Code
Aug 19, 2016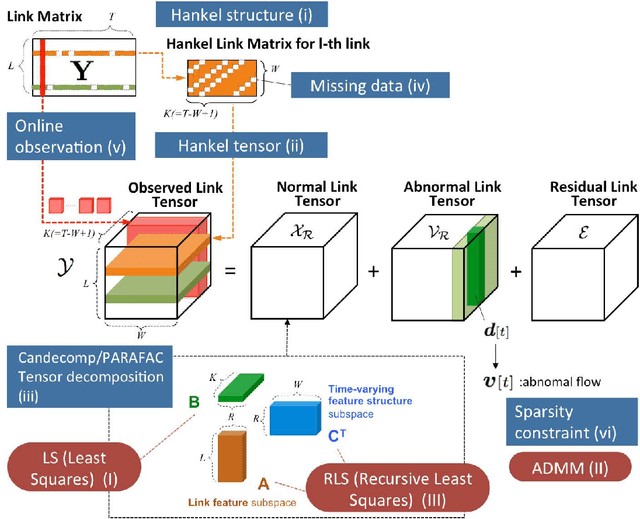

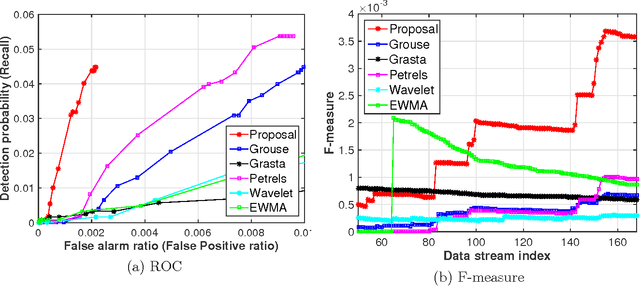
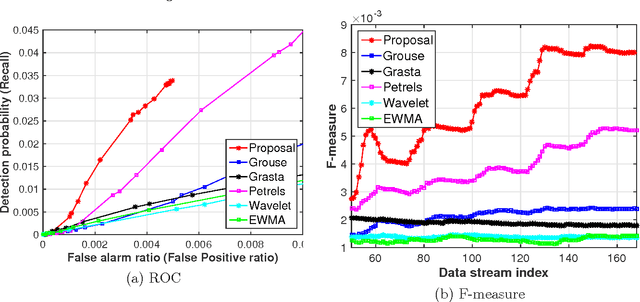
This paper addresses network anomography, that is, the problem of inferring network-level anomalies from indirect link measurements. This problem is cast as a low-rank subspace tracking problem for normal flows under incomplete observations, and an outlier detection problem for abnormal flows. Since traffic data is large-scale time-structured data accompanied with noise and outliers under partial observations, an efficient modeling method is essential. To this end, this paper proposes an online subspace tracking of a Hankelized time-structured traffic tensor for normal flows based on the Candecomp/PARAFAC decomposition exploiting the recursive least squares (RLS) algorithm. We estimate abnormal flows as outlier sparse flows via sparsity maximization in the underlying under-constrained linear-inverse problem. A major advantage is that our algorithm estimates normal flows by low-dimensional matrices with time-directional features as well as the spatial correlation of multiple links without using the past observed measurements and the past model parameters. Extensive numerical evaluations show that the proposed algorithm achieves faster convergence per iteration of model approximation, and better volume anomaly detection performance compared to state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge