Network Pruning for Low-Rank Binary Indexing
Paper and Code
May 14, 2019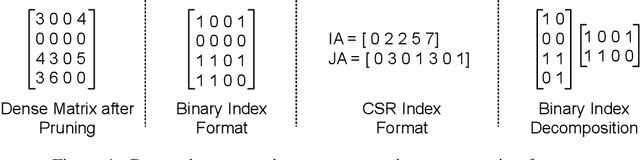
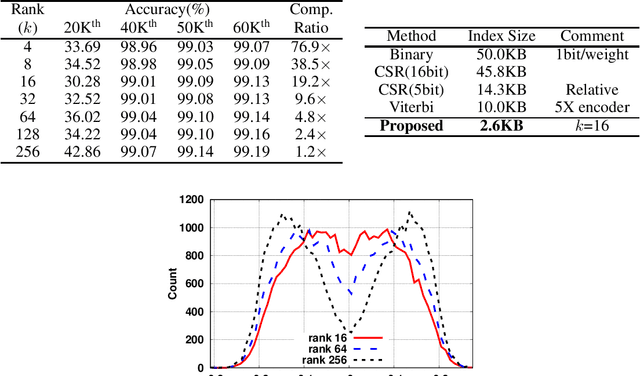
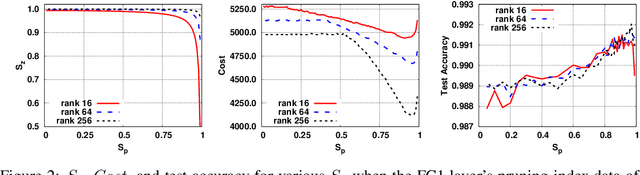
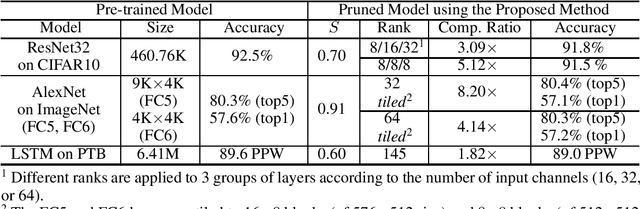
Pruning is an efficient model compression technique to remove redundancy in the connectivity of deep neural networks (DNNs). Computations using sparse matrices obtained by pruning parameters, however, exhibit vastly different parallelism depending on the index representation scheme. As a result, fine-grained pruning has not gained much attention due to its irregular index form leading to large memory footprint and low parallelism for convolutions and matrix multiplications. In this paper, we propose a new network pruning technique that generates a low-rank binary index matrix to compress index data while decompressing index data is performed by simple binary matrix multiplication. This proposed compression method finds a particular fine-grained pruning mask that can be decomposed into two binary matrices. We also propose a tile-based factorization technique that not only lowers memory requirements but also enhances compression ratio. Various DNN models can be pruned with much fewer indexes compared to previous sparse matrix formats while maintaining the same pruning rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge