Network Modeling of Short Over-Dispersed Spike-Counts: A Hierarchical Parametric Empirical Bayes Framework

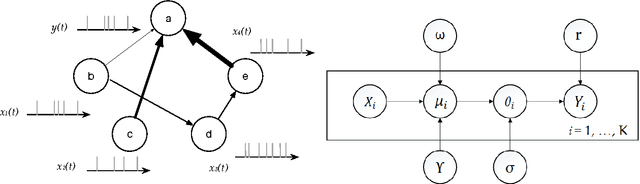
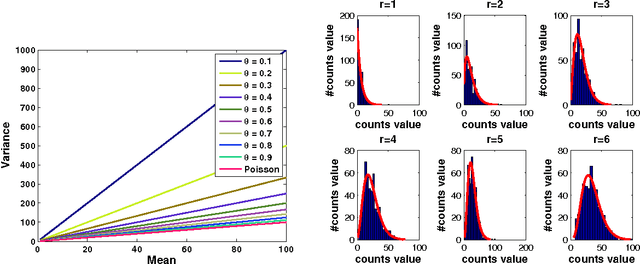
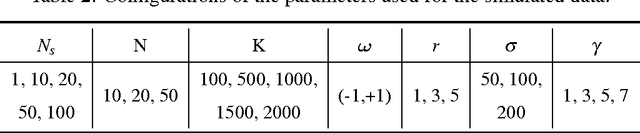
Accurate statistical models of neural spike responses can characterize the information carried by neural populations. Yet, challenges in recording at the level of individual neurons commonly results in relatively limited samples of spike counts, which can lead to model overfitting. Moreover, current models assume spike counts to be Poisson-distributed, which ignores the fact that many neurons demonstrate over-dispersed spiking behavior. The Negative Binomial Generalized Linear Model (NB-GLM) provides a powerful tool for modeling over-dispersed spike counts. However, maximum likelihood based standard NB-GLM leads to unstable and inaccurate parameter estimations. Thus, we propose a hierarchical parametric empirical Bayes method for estimating the parameters of the NB-GLM. Our method integrates Generalized Linear Models (GLMs) and empirical Bayes theory to: (1) effectively capture over-dispersion nature of spike counts from retinal ganglion neural responses; (2) significantly reduce mean square error of parameter estimations when compared to maximum likelihood based method for NB-GLMs; (3) provide an efficient alternative to fully Bayesian inference with low computational cost for hierarchical models; and (4) give insightful findings on both neural interactions and spiking behaviors of real retina cells. We apply our approach to study both simulated data and experimental neural data from the retina. The simulation results indicate the new framework can efficiently and accurately retrieve the weights of functional connections among neural populations and predict mean spike counts. The results from the retinal datasets demonstrate the proposed method outperforms both standard Poisson and Negative Binomial GLMs in terms of the predictive log-likelihood of held-out data.