Network Connectivity--Information Freshness Tradeoff in Information Dissemination Over Networks
Paper and Code
May 29, 2024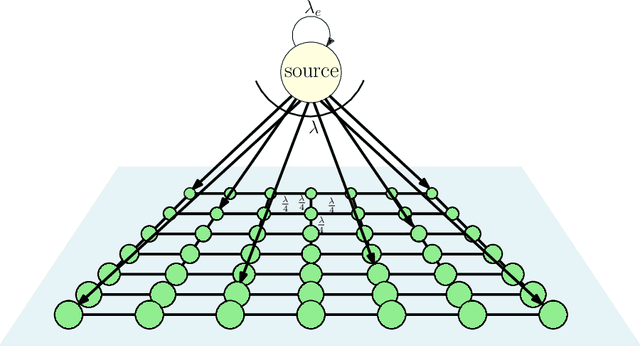

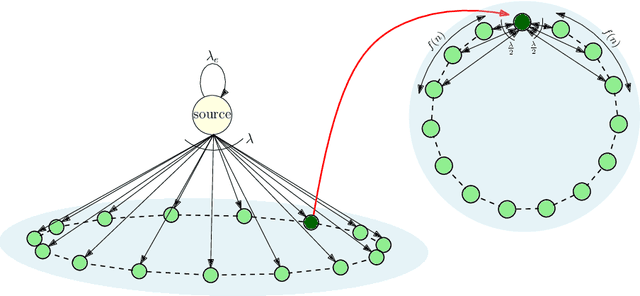

We consider a gossip network consisting of a source generating updates and $n$ nodes connected according to a given graph structure. The source keeps updates of a process, that might be generated or observed, and shares them with the gossiping network. The nodes in the network communicate with their neighbors and disseminate these version updates using a push-style gossip strategy. We use the version age metric to quantify the timeliness of information at the nodes. We first find an upper bound for the average version age for a set of nodes in a general network. Using this, we find the average version age scaling of a node in several network graph structures, such as two-dimensional grids, generalized rings and hyper-cubes. Prior to our work, it was known that when $n$ nodes are connected on a ring the version age scales as $O(n^{\frac{1}{2}})$, and when they are connected on a fully-connected graph the version age scales as $O(\log n)$. Ours is the first work to show an age scaling result for a connectivity structure other than the ring and the fully-connected network, which constitute the two extremes of network connectivity. Our work helps fill the gap between these two extremes by analyzing a large variety of graphs with intermediate connectivity, thus providing insight into the relationship between the connectivity structure of the network and the version age, and uncovering a network connectivity--information freshness tradeoff.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge