Nearly Horizon-Free Offline Reinforcement Learning
Paper and Code
Mar 25, 2021
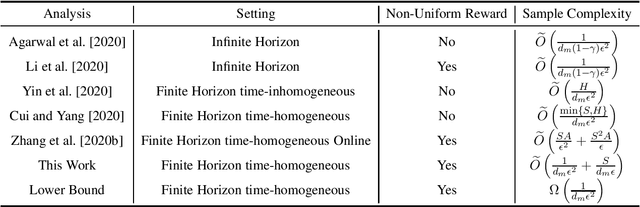
We revisit offline reinforcement learning on episodic time-homogeneous tabular Markov Decision Processes with $S$ states, $A$ actions and planning horizon $H$. Given the collected $N$ episodes data with minimum cumulative reaching probability $d_m$, we obtain the first set of nearly $H$-free sample complexity bounds for evaluation and planning using the empirical MDPs: 1.For the offline evaluation, we obtain an $\tilde{O}\left(\sqrt{\frac{1}{Nd_m}} \right)$ error rate, which matches the lower bound and does not have additional dependency on $\poly\left(S,A\right)$ in higher-order term, that is different from previous works~\citep{yin2020near,yin2020asymptotically}. 2.For the offline policy optimization, we obtain an $\tilde{O}\left(\sqrt{\frac{1}{Nd_m}} + \frac{S}{Nd_m}\right)$ error rate, improving upon the best known result by \cite{cui2020plug}, which has additional $H$ and $S$ factors in the main term. Furthermore, this bound approaches the $\Omega\left(\sqrt{\frac{1}{Nd_m}}\right)$ lower bound up to logarithmic factors and a high-order term. To the best of our knowledge, these are the first set of nearly horizon-free bounds in offline reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge