Near-Optimal Sparse Allreduce for Distributed Deep Learning
Paper and Code
Jan 19, 2022
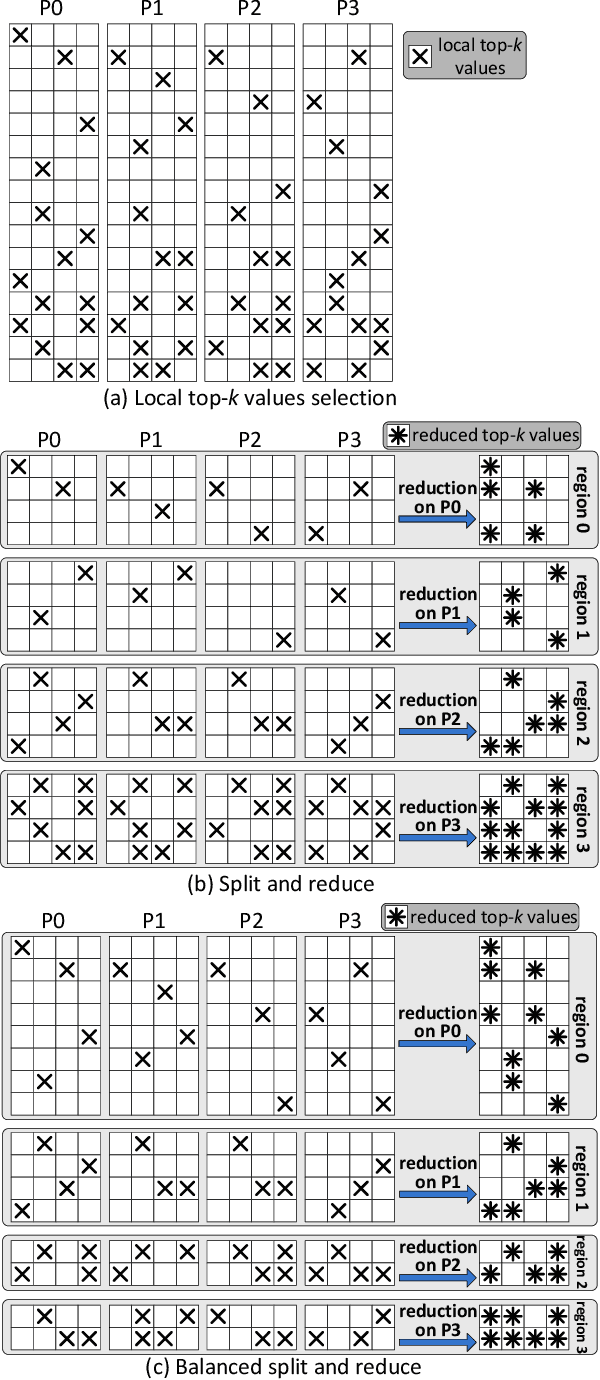
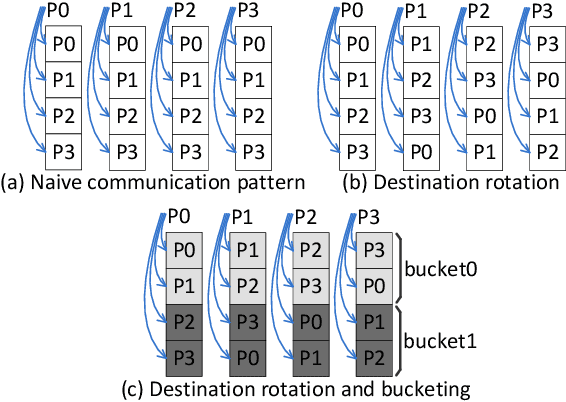

Communication overhead is one of the major obstacles to train large deep learning models at scale. Gradient sparsification is a promising technique to reduce the communication volume. However, it is very challenging to obtain real performance improvement because of (1) the difficulty of achieving an scalable and efficient sparse allreduce algorithm and (2) the sparsification overhead. This paper proposes O$k$-Top$k$, a scheme for distributed training with sparse gradients. O$k$-Top$k$ integrates a novel sparse allreduce algorithm (less than 6$k$ communication volume which is asymptotically optimal) with the decentralized parallel Stochastic Gradient Descent (SGD) optimizer, and its convergence is proved. To reduce the sparsification overhead, O$k$-Top$k$ efficiently selects the top-$k$ gradient values according to an estimated threshold. Evaluations are conducted on the Piz Daint supercomputer with neural network models from different deep learning domains. Empirical results show that O$k$-Top$k$ achieves similar model accuracy to dense allreduce. Compared with the optimized dense and the state-of-the-art sparse allreduces, O$k$-Top$k$ is more scalable and significantly improves training throughput (e.g., 3.29x-12.95x improvement for BERT on 256 GPUs).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge