Navigating the Semantic Horizon using Relative Neighborhood Graphs
Paper and Code
Jan 12, 2015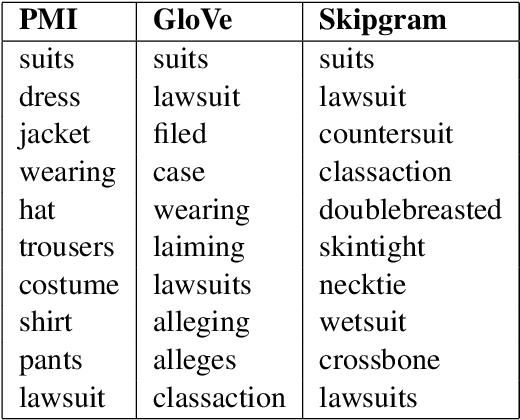

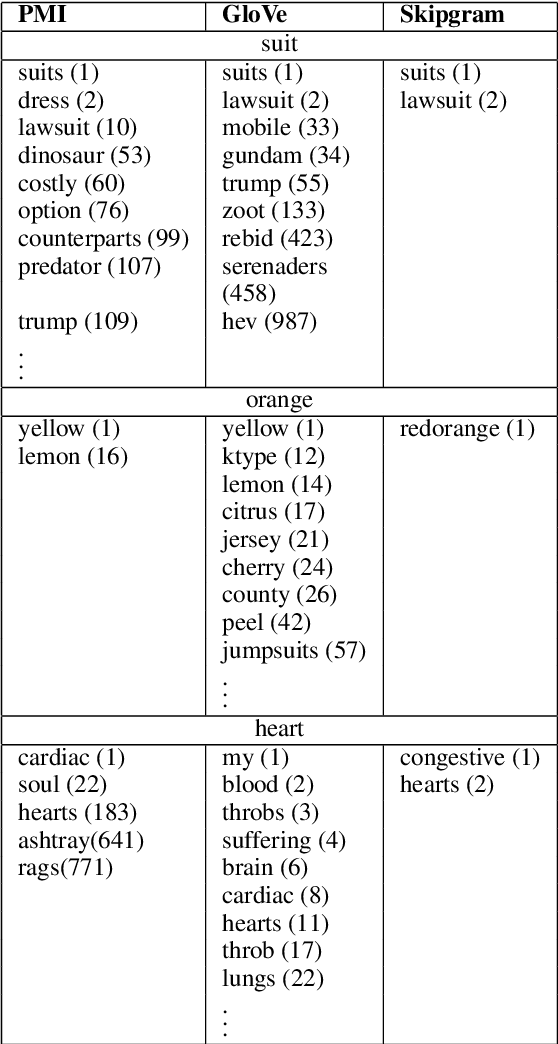

This paper is concerned with nearest neighbor search in distributional semantic models. A normal nearest neighbor search only returns a ranked list of neighbors, with no information about the structure or topology of the local neighborhood. This is a potentially serious shortcoming of the mode of querying a distributional semantic model, since a ranked list of neighbors may conflate several different senses. We argue that the topology of neighborhoods in semantic space provides important information about the different senses of terms, and that such topological structures can be used for word-sense induction. We also argue that the topology of the neighborhoods in semantic space can be used to determine the semantic horizon of a point, which we define as the set of neighbors that have a direct connection to the point. We introduce relative neighborhood graphs as method to uncover the topological properties of neighborhoods in semantic models. We also provide examples of relative neighborhood graphs for three well-known semantic models; the PMI model, the GloVe model, and the skipgram model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge