Natural Statistics of Network Activations and Implications for Knowledge Distillation
Paper and Code
Jun 01, 2021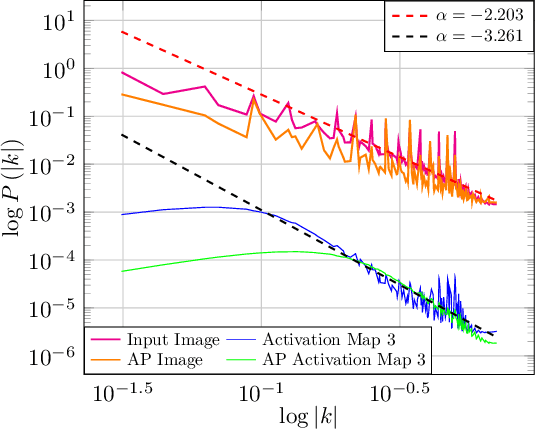
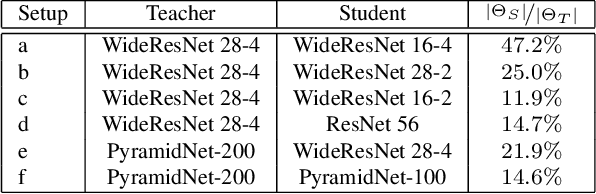
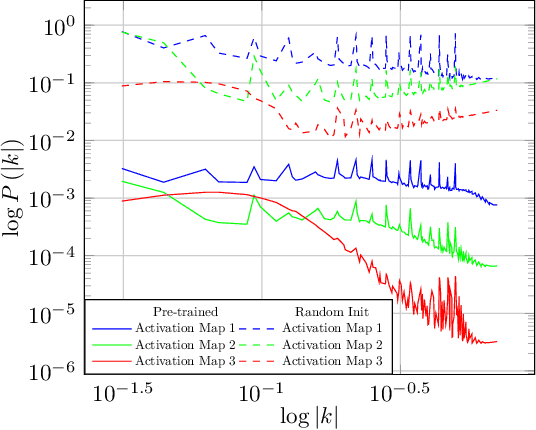

In a matter that is analog to the study of natural image statistics, we study the natural statistics of the deep neural network activations at various layers. As we show, these statistics, similar to image statistics, follow a power law. We also show, both analytically and empirically, that with depth the exponent of this power law increases at a linear rate. As a direct implication of our discoveries, we present a method for performing Knowledge Distillation (KD). While classical KD methods consider the logits of the teacher network, more recent methods obtain a leap in performance by considering the activation maps. This, however, uses metrics that are suitable for comparing images. We propose to employ two additional loss terms that are based on the spectral properties of the intermediate activation maps. The proposed method obtains state of the art results on multiple image recognition KD benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge