Natural Evolutionary Strategies for Variational Quantum Computation
Paper and Code
Nov 30, 2020
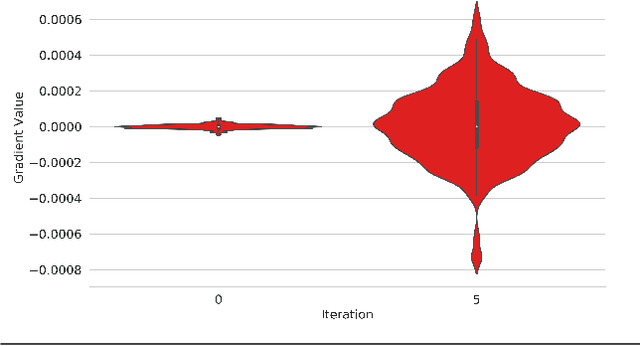
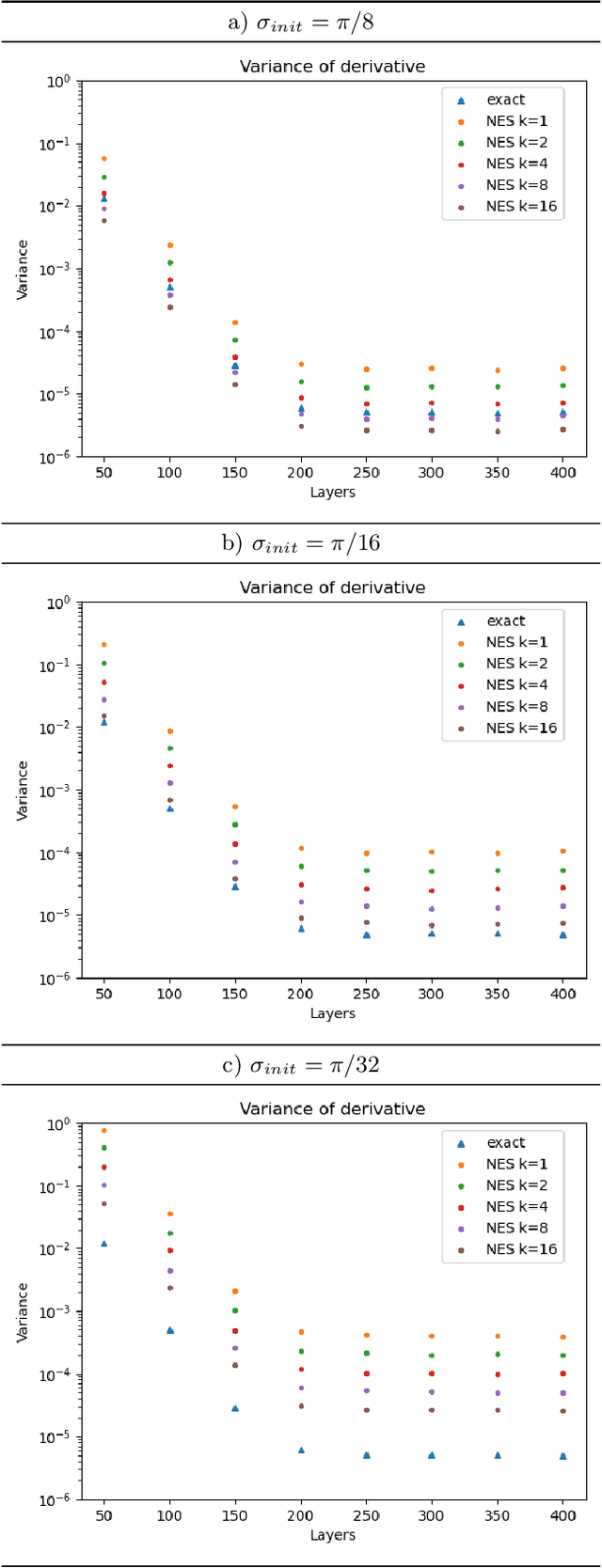
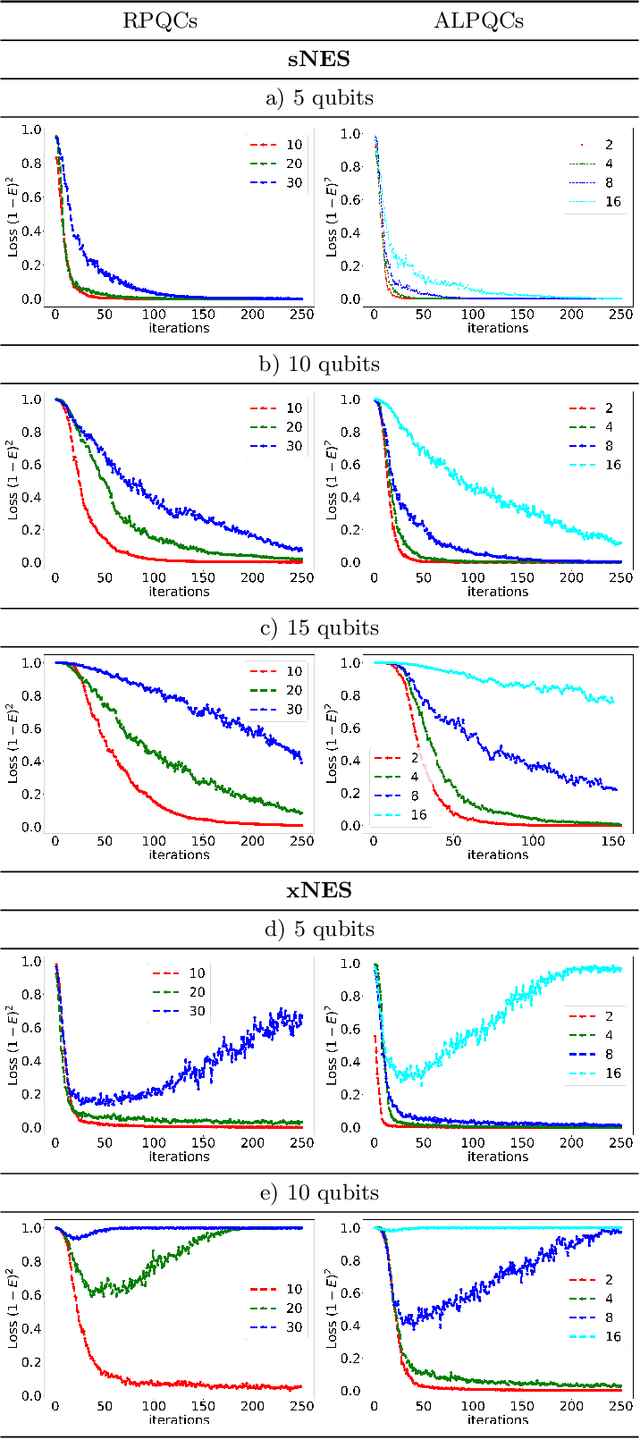
Natural evolutionary strategies (NES) are a family of gradient-free black-box optimization algorithms. This study illustrates their use for the optimization of randomly-initialized parametrized quantum circuits (PQCs) in the region of vanishing gradients. We show that using the NES gradient estimator the exponential decrease in variance can be alleviated. We implement two specific approaches, the exponential and separable natural evolutionary strategies, for parameter optimization of PQCs and compare them against standard gradient descent. We apply them to two different problems of ground state energy estimation using variational quantum eigensolver (VQE) and state preparation with circuits of varying depth and length. We also introduce batch optimization for circuits with larger depth to extend the use of evolutionary strategies to a larger number of parameters. We achieve accuracy comparable to state-of-the-art optimization techniques in all the above cases with a lower number of circuit evaluations. Our empirical results indicate that one can use NES as a hybrid tool in tandem with other gradient-based methods for optimization of deep quantum circuits in regions with vanishing gradients.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge