N-LIMB: Neural Limb Optimization for Efficient Morphological Design
Paper and Code
Jul 24, 2022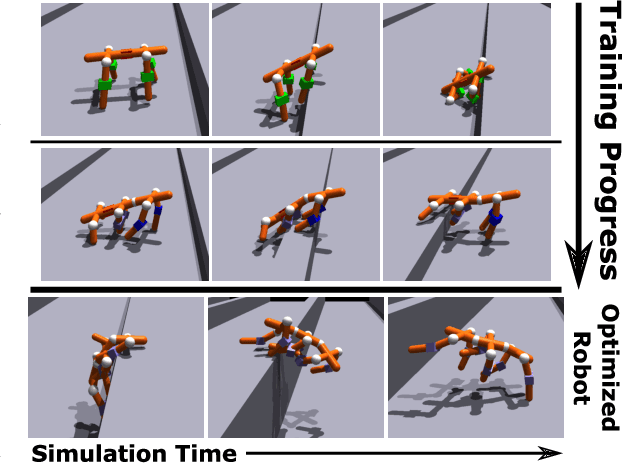
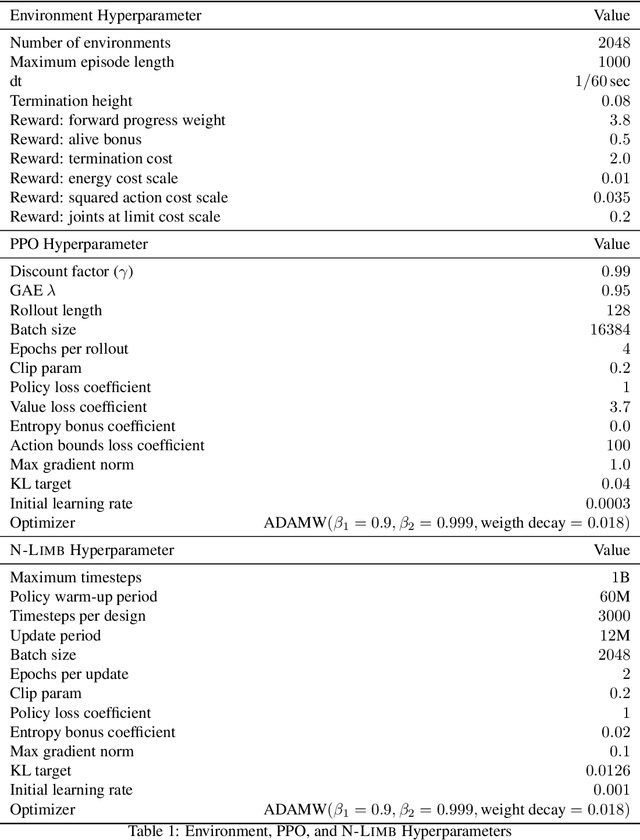
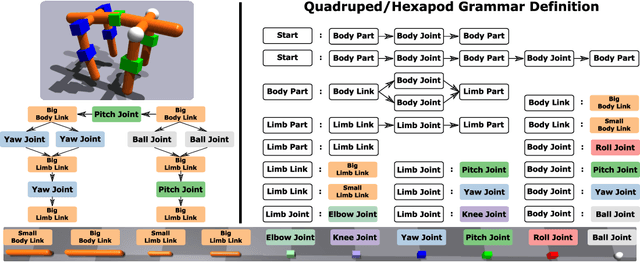
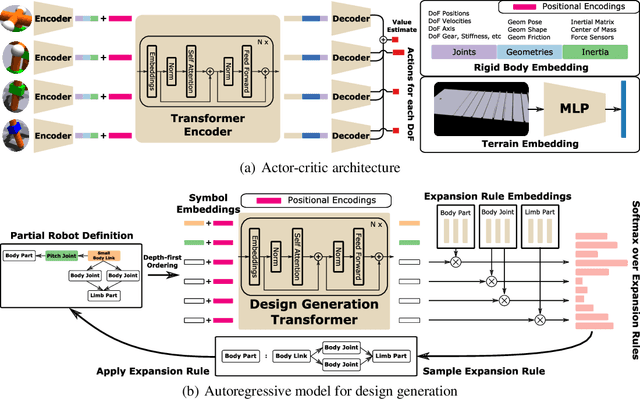
A robot's ability to complete a task is heavily dependent on its physical design. However, identifying an optimal physical design and its corresponding control policy is inherently challenging. The freedom to choose the number of links, their type, and how they are connected results in a combinatorial design space, and the evaluation of any design in that space requires deriving its optimal controller. In this work, we present N-LIMB, an efficient approach to optimizing the design and control of a robot over large sets of morphologies. Central to our framework is a universal, design-conditioned control policy capable of controlling a diverse sets of designs. This policy greatly improves the sample efficiency of our approach by allowing the transfer of experience across designs and reducing the cost to evaluate new designs. We train this policy to maximize expected return over a distribution of designs, which is simultaneously updated towards higher performing designs under the universal policy. In this way, our approach converges towards a design distribution peaked around high-performing designs and a controller that is effectively fine-tuned for those designs. We demonstrate the potential of our approach on a series of locomotion tasks across varying terrains and show the discovery novel and high-performing design-control pairs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge