Multiview Learning of Weighted Majority Vote by Bregman Divergence Minimization
Paper and Code
May 25, 2018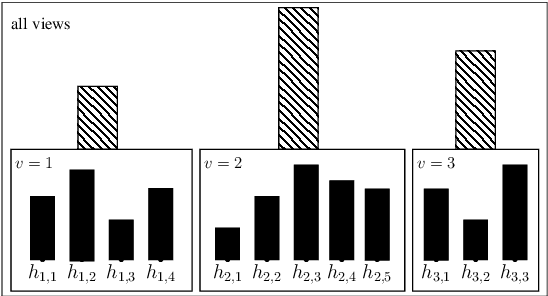

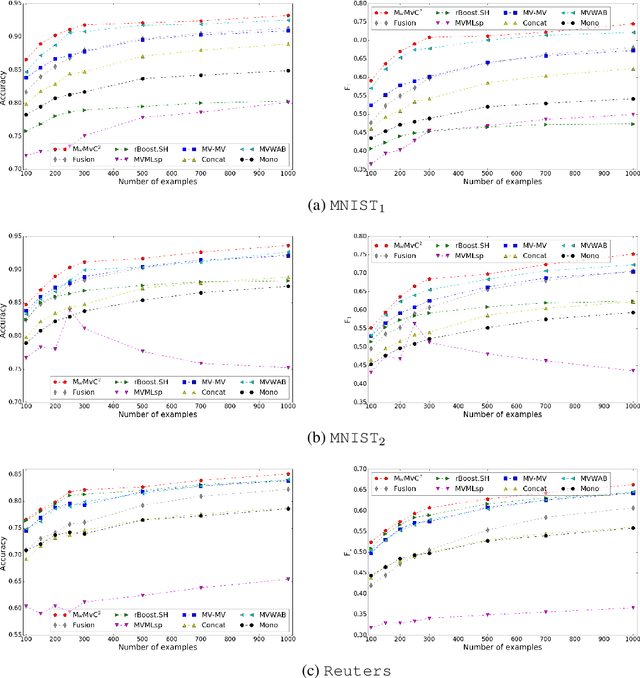
We tackle the issue of classifier combinations when observations have multiple views. Our method jointly learns view-specific weighted majority vote classifiers (i.e. for each view) over a set of base voters, and a second weighted majority vote classifier over the set of these view-specific weighted majority vote classifiers. We show that the empirical risk minimization of the final majority vote given a multiview training set can be cast as the minimization of Bregman divergences. This allows us to derive a parallel-update optimization algorithm for learning our multiview model. We empirically study our algorithm with a particular focus on the impact of the training set size on the multiview learning results. The experiments show that our approach is able to overcome the lack of labeled information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge