$β$-Multivariational Autoencoder for Entangled Representation Learning in Video Frames
Paper and Code
Nov 22, 2022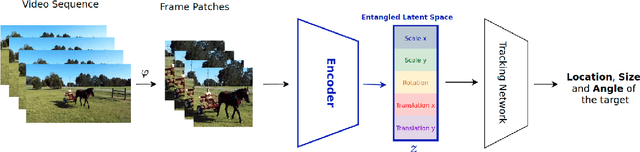
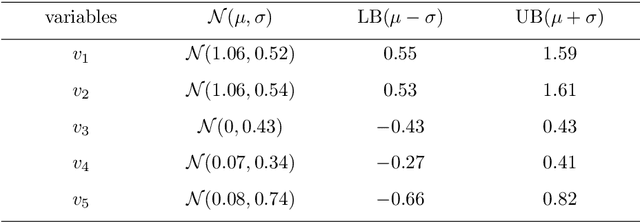
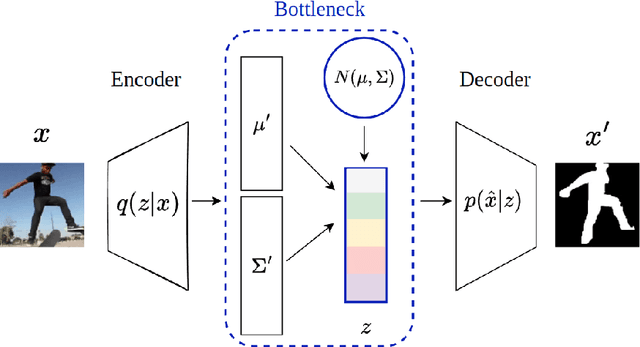
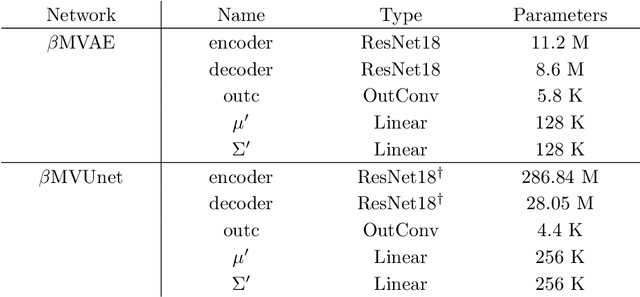
It is crucial to choose actions from an appropriate distribution while learning a sequential decision-making process in which a set of actions is expected given the states and previous reward. Yet, if there are more than two latent variables and every two variables have a covariance value, learning a known prior from data becomes challenging. Because when the data are big and diverse, many posterior estimate methods experience posterior collapse. In this paper, we propose the $\beta$-Multivariational Autoencoder ($\beta$MVAE) to learn a Multivariate Gaussian prior from video frames for use as part of a single object-tracking in form of a decision-making process. We present a novel formulation for object motion in videos with a set of dependent parameters to address a single object-tracking task. The true values of the motion parameters are obtained through data analysis on the training set. The parameters population is then assumed to have a Multivariate Gaussian distribution. The $\beta$MVAE is developed to learn this entangled prior $p = N(\mu, \Sigma)$ directly from frame patches where the output is the object masks of the frame patches. We devise a bottleneck to estimate the posterior's parameters, i.e. $\mu', \Sigma'$. Via a new reparameterization trick, we learn the likelihood $p(\hat{x}|z)$ as the object mask of the input. Furthermore, we alter the neural network of $\beta$MVAE with the U-Net architecture and name the new network $\beta$Multivariational U-Net ($\beta$MVUnet). Our networks are trained from scratch via over 85k video frames for 24 ($\beta$MVUnet) and 78 ($\beta$MVAE) million steps. We show that $\beta$MVUnet enhances both posterior estimation and segmentation functioning over the test set. Our code and the trained networks are publicly released.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge