Multiscale Dubuc: A New Similarity Measure for Time Series
Paper and Code
Nov 15, 2024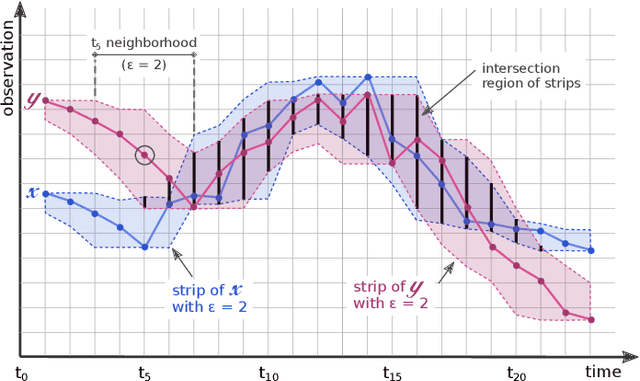
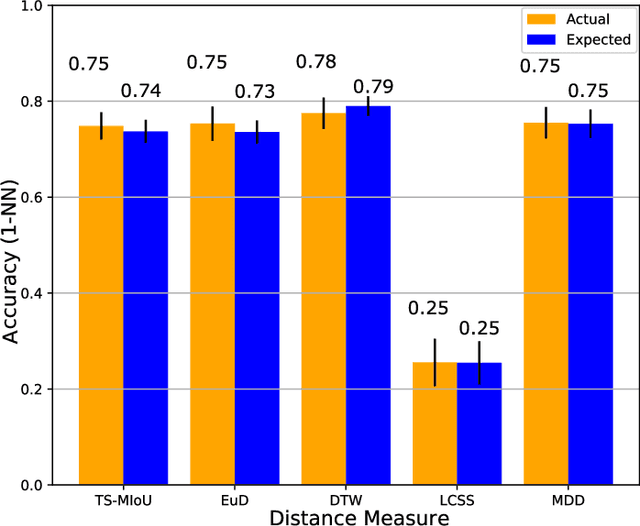
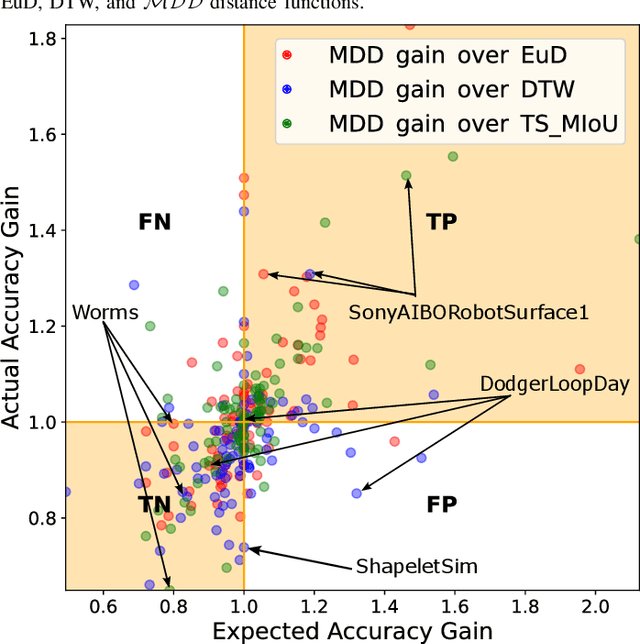
Quantifying similarities between time series in a meaningful way remains a challenge in time series analysis, despite many advances in the field. Most real-world solutions still rely on a few popular measures, such as Euclidean Distance (EuD), Longest Common Subsequence (LCSS), and Dynamic Time Warping (DTW). The strengths and weaknesses of these measures have been studied extensively, and incremental improvements have been proposed. In this study, however, we present a different similarity measure that fuses the notion of Dubuc's variation from fractal analysis with the Intersection-over-Union (IoU) measure which is widely used in object recognition (also known as the Jaccard Index). In this proof-of-concept paper, we introduce the Multiscale Dubuc Distance (MDD) measure and prove that it is a metric, possessing desirable properties such as the triangle inequality. We use 95 datasets from the UCR Time Series Classification Archive to compare MDD's performance with EuD, LCSS, and DTW. Our experiments show that MDD's overall success, without any case-specific customization, is comparable to DTW with optimized window sizes per dataset. We also highlight several datasets where MDD's performance improves significantly when its single parameter is customized. This customization serves as a powerful tool for gauging MDD's sensitivity to noise. Lastly, we show that MDD's running time is linear in the length of the time series, which is crucial for real-world applications involving very large datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge