Multiplicative Logit Adjustment Approximates Neural-Collapse-Aware Decision Boundary Adjustment
Paper and Code
Sep 26, 2024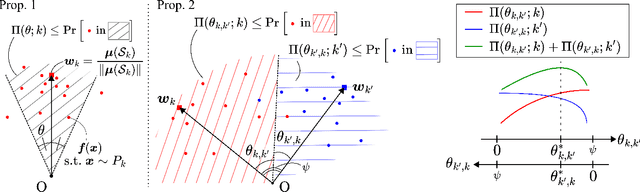

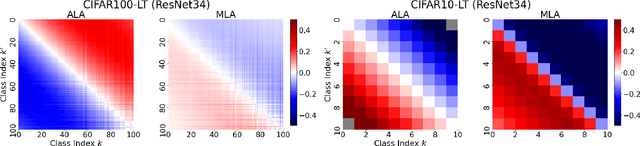

Real-world data distributions are often highly skewed. This has spurred a growing body of research on long-tailed recognition to address this imbalance in training classification models. Among the methods studied, multiplicative logit adjustment (MLA) stands out as a simple and effective method. However, it lacks theoretical guarantees, which raises concerns about the optimality of its adjustment method. We provide a theoretical justification for the effectiveness of MLA with the following two-step theory. First, we develop a theory that adjusts optimal decision boundaries by estimating feature spread on the basis of neural collapse. Then, we demonstrate that MLA approximates this optimal method. Additionally, through experiments on long-tailed datasets, we illustrate the practical usefulness of MLA under more realistic conditions. We also offer experimental insights to guide the tuning of MLA's hyperparameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge