Multiple-Source Adaptation for Regression Problems
Paper and Code
Nov 14, 2017

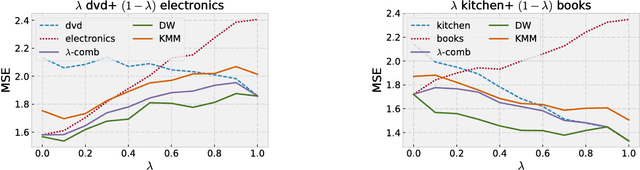

We present a detailed theoretical analysis of the problem of multiple-source adaptation in the general stochastic scenario, extending known results that assume a single target labeling function. Our results cover a more realistic scenario and show the existence of a single robust predictor accurate for \emph{any} target mixture of the source distributions. Moreover, we present an efficient and practical optimization solution to determine the robust predictor in the important case of squared loss, by casting the problem as an instance of DC-programming. We report the results of experiments with both an artificial task and a sentiment analysis task. We find that our algorithm outperforms competing approaches by producing a single robust model that performs well on any target mixture distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge